LISTA DE DISCIPLINAS

| MA111 - Cálculo I | Funções | Modos de representar funções

Modos de representar funções

Selecione os exercícios por

Dificuldade

Categoria

Outros

Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.

923   

Esboce o gráfico de $f(x) =x^2+6x+10.$ Use completamento de quadrados.


646   

Seja $f\left( x\right) =\frac{1+x}{1-x}$. Mostre que $f\left( \frac{1}{1+x}\right) =\frac{2+x}{x}$, $f\left( \frac{1}{1-x}\right) =\frac{x-2}{x}$, $f\left( -x\right) =\frac{1}{f\left( x\right) }$, $f\left( 1/x\right)=-f\left( x\right) $ e que $f\left( f\left( x\right) \right) =-1/x$.

660   

Considere o gráfico da função $f$:


$f\left( x\right) =\left\{\begin{array}{c}-2x-2,-4\leq x\leq -2 \\x+4,-2\leq x\leq 1 \\6-x,1\leq x\leq 4\end{array}\right.$

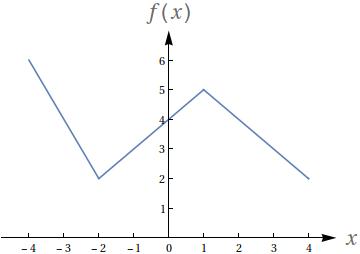
fig_modos_representar_funcoes_26.png

Esboce, a partir deste, os gráficos das seguintes funções:

  1. $y=f\left( x+4\right) $

  2. $y=f\left( x\right) +4$

  3. $y=2f\left( x\right) $

  4. $y=-\dfrac{1}{2}f\left( x\right) +3.$

920   

Um fabricante de refrigerante quer produzir latas cilíndricas para seu produto. A lata dever ter um volume de $360 ml$. Expresse a área superficial total da lata em função do seu raio e dê o domínio da função.


Sejam $r$ o raio da base do cilindro e $h$ a sua altura. O volume $V$ do cilindro é dado por $V=\pi r^2 h$. Como $V=360$, obtemos $\pi r^2 h=360$, isto é, $h=\dfrac{360}{\pi r^2}$. A área superficial $A$ do cilindro é $A=2 \pi r^2+2 \pi r h$. Substituindo $h$ por $\dfrac{360}{\pi r^2}$ chegamos a $A=2 \pi r^2+2 \pi r \dfrac{360}{\pi r^2}$, ou seja, $A=2 \pi r^2+ \dfrac{360}{r}$. O domínio da função $A(r)$ é $\mathbb{R}^+$.


647   

Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.

  1. $f(x)=\sin x$

  2. $f(x)=\cos x$


  1. A função $\sin x$ é ímpar pois $f(-x) = \sin (-x) = -\sin(x) = -f(x)$.
  1. A função $\cos x$ é par pois $f(-x) = \cos (-x) = \cos(x) = f(x)$.

640   

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

  1. $y=\sqrt{x-2}$

  2. $y=\sqrt{2-x}$


  1. O domínio de $y$ é o conjunto de números reais em que o valor dentro da raiz é positivo. Calculando esses valores:
    $x-2 > 0 \Rightarrow x > 2$.
    Portanto o domínio de $y$ é: $\{x \in \mathbb{R}; x >2\}$.
  2. O domínio de $y$ é o conjunto de números reais em que o valor dentro da raiz é positivo. Calculando esses valores:
    $2-x > 0 \Rightarrow x < 2$.
    Portanto o domínio de $y$ é: $\{x \in \mathbb{R}; x <2\}$.

655   

Esboce o gráfico de cada uma das funções abaixo.

  1. $y=\sqrt{9-(2-x)^{2}}$

  2. $y=7/2-\sqrt{13-(2+x)^{2}}$

653   

Esboce o gráfico de cada uma das funções abaixo.

  1. $y=-\sqrt{7-x^{2}}$

  2. $y=1+\sqrt{10-x^{2}}$

924   

Uma caixa retangular aberta com volume de $2 m^3$ tem a base quadrada. Expresse a área superficial da caixa como função de um dos lados da base.



Sejam $x$ a medida do lado da base da caixa e $z$ sua altura. O volume $V$ dessa caixa é dado por $V=x^2z$. Como $V=2$, temos $z=\dfrac{2}{x^2}$. A área superficial $A$ da caixa (sem tampa!) é $A=x^2+4xz$. Substituindo $z$ por $\dfrac{2}{x^2}$ obtemos $A=x^2+\dfrac{8}{x}$. 

919   

Esboce o gráfico de $f(x) = |x-1|+3.$


636   

Sejam $f\left( x\right) =\frac{x^{2}-25}{x^{2}-1}$ e $g\left(x\right) =\sqrt{x}$. Dê o domínio das seguintes funções: $f,$ $g$, $f\circ g$ e $g\circ f$.

637   

Dada a função $f\left( x\right) =$ $\left| x\right| -2x$, calcule $f\left( -1\right) $, $f\left( 1/2\right) $, $f\left( -2/3\right) $. Mostre que $f\left( \left| a\right| \right) =-\left| a\right| $.

652   

Esboce o gráfico de cada uma das funções abaixo.

  1. $y=\frac{2|x+1|}{3}$

  2. $y=\sqrt{5-x^{2}}$

925   

A área superficial de uma caixa retangular fechada de base quadrada é igual a $20 m^2$. Determine o volume desta caixa em função do comprimento do lado de sua base.

635   

Se $f(x+1)=\frac{x-1}{\pi -x},$ ache $f\left( x\right) $ e encontre o domínio de $f$.


Calculando $f((x-1)+1)$:
$f((x-1)+1)=\dfrac{(x-1)-1}{\pi-(x-1)}$
$f(x) = \dfrac{x-2}{\pi+1-x}$.
O domínio de $f$ é o conjunto de números reais menos os pontos em que o denominador é zero. Calculando esses valores:
$\pi + 1 - x  = 0 \Rightarrow x = \pi + 1$.
Portanto o domínio de $f$ é: $\{x \in \mathbb{R}; x \neq \pi + 1\}$.

654   

Esboce o gráfico de cada uma das funções abaixo.

  1. $y=2-\sqrt{16-x^{2}}$

  2. $y=-1+\sqrt{6-(x-1)^{2}}$

639   

Sejam $f(x)=\sqrt{\displaystyle{\frac{x+3}{x-3}}}$ e $g(x)=\displaystyle{\frac{\sqrt{x+3}}{\sqrt{x-3}}}$. Determine o domínio da função $f$ e o domínio da função $g$. É verdade que $f=g$?

651   

Sejam $f(x)=\frac{x^{2}-25}{x^{2}-1}$ e $g(x)=\sqrt{x}$. Dê o domínio de cada uma das funções $f$, $g$, $f\circ g$ e $g\circ f$.

650   

Se $f(x+1)=\frac{x-1}{\pi -x}$, ache $f(x)$ e encontre o domínio de $f$.

641   

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

  1. $y=\sqrt{x^{2}-9}$

  2. $y=\sqrt{-x}$

  1. $\{x \in \mathbb{R}; x<-3 \text{ ou }x>3\}$.
  2. $\{x \in \mathbb{R}; x<0\}$.

638   

Seja $f\left( x\right) =\left| x\right| -x$. Mostre que $f\left( x\right) =0$ para $x\geq 0$ e $f\left( x\right) =-2x$ para $x<0$. Faça o gráfico dessa função.

648   

Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.

  1. $f(x)=\tan x$

  2. $f(x)=x^{2}+1$

645   

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

  1. $y=\sqrt{x^{2}-4x+3}$

  2. $y=\sqrt{x^{2}+3x-10}$

657   

Seja $f(x)=\frac{1+x}{1-x}$. Mostre que $f\left(\frac{1}{1+x}\right)=\frac{2+x}{x}$, $f\left(\frac{1}{1-x}\right)=\frac{x-2}{x}$, $f(-x)=\frac{1}{f(x)}$, $f(1/x)=-f(x)$,  $f(f(x))=-1/x$.

642   

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

  1. $y=\sqrt[3]{x}$

  2. $y=\sqrt[3]{-x}$

  1. $\mathbb{R}$.
  2. $\mathbb{R}$.

643   

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

  1. $y=\sqrt[3]{x-2}$

  2. $y=\displaystyle{\frac{1}{x^{2}-4}}$

644   

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

  1. $y=\sqrt{x+5}$

  2. $y=\sqrt{3-2x}$


  1. $[-5,\infty[$
  2. $]-\infty,\frac{3}{2}]$

921   

Esboce os gráficos de $f(x) =x^2-1$ e $ g(x) = x^2 +1.$

656   

Esboce o gráfico de cada uma das funções abaixo.

  1. $y=|x|+x$

  2. $y=1-x$ se $x\leq 0$ e $y=\sqrt{1-x^{2}}$ se $0\leq x\leq 1$.

922   

Partindo do gráfico de $h(x)=x^2$, esboce os gráficos de $f(x) =(x-1)^2$ e $ g(x) = (x +1)^2.$


649   

Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.

  1. $f(x)=x^{3}+x$

  2. $f(x)=x^{4}+2x^{3}+x^{2}$


  1. $f(-x)=(-x)^{3}+(-x) = -x^3-x = -(x^3+x) = -f(x)$, logo a função é ímpar.
  1. $f(-x)=(-x)^{4}+2(-x)^{3}+(-x)^{2} = x^4-2x^3+x^2$, que não é igual a $f(x)$ nem $-f(x)$, logo a função não é par nem ímpar.