Taxas Relacionadas
Taxas relacionadas - Problema dos carrinhos
Problema: Dois carrinhos, $A$ e $B$, estão conectados por uma corda de 39 pés de comprimento que passa por uma polia. O ponto $Q$ está no chão, 12 metros abaixo da polia e entre os carrinhos. O carrinho $A$ está sendo puxado para longe de $Q$ a uma velocidade de 2 pés/s. Quão rápido o carrinho $B$ está se movendo na direção de $Q$ no instante em que o carrinho $A$ está a 5 pés de distância de $Q$?
Certifique-se de que você escreveu um modelo dinâmico e use diferenciação implícita para diferenciar ambos os lados da sua equação com respeito à variável apropriada. Responda a questão anterior e confira seu resultado no aplicativo abaixo.
Observação 1: Você pode criar diferentes animações mudando a velocidade do carrinho $A$ se desejar. As unidades de $da/dt$ são $pés/s$.
Observação 2: A criação deste aplicativo foi inspirada em um problema de Taxas Relacionadas retirado da Seção 3.9 do livro Calculus (Early Transcendentals), 7a. edição, de J. Stewart. Este problema já aparecia em textos anteriores dele.
Aplicativo em inglês.
Taxas relacionadas - Uma escada que cai
Suponha que uma escada tem 10 pés de altura e, de algum modo, está encostada verticalmente a uma parede.
Alguém chuta a escada de modo que sua base começa a se distanciar da parede a uma taxa de 3 pés/s. Vá em frente e chute a escada, clicando em Kick Ladder!
A que taxa a altura $h$, em que o topo da escada toca a parede, está variando quando a base da escada está a 6 pés da parede? E quando a base está a 9 pés da parede?
Use derivação implícita para determinar as respostas das duas questões anteriores e, então, confira os valores aproximados dos seus resultados com os valores do aplicativo abaixo.
Na verdade, em qualquer momento, você pode ajustar os valores de $\dfrac{dx}{dt}$.
Questões:
Por que o valor de $\dfrac{dh}{dt}$ é sempre negativo, exceto em $x=0$? Explique.
Quão longe a base da escada deve estar da parede para que $\dfrac{dx}{dt}=\left|\dfrac{dh}{dt}\right|$? Você pode tentar adivnhar e conferir sua resposta no aplicativo. Depois, certifique-se que você é capaz de obter a solução exata usando Cálculo.
Aplicativo em inglês.
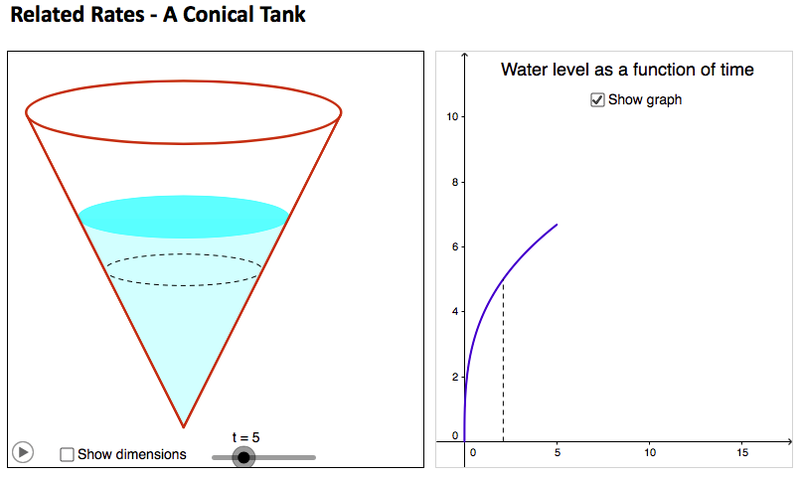
Um tanque cônico
Observe como o nível da água de um tanque cônico varia ao longo do tempo.
Applet em inglês
Outros applets disponíveis na página do Prof. Marc Renault.

