Volume de sólido obtido pela rotação, em torno do eixo x e do eixo y
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Calcule o volume da esfera de raio $R$ de duas maneiras diferentes: a primeira através da rotação de um gráfico em torno do eixo $x$ e a segunda através da rotação de um gráfico em torno do eixo $y$.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2},0\leq x\leq 2,y=4,x-0$ ao redor do eixo $y.$

Considere a região no plano com limite inferior dado por $y=1+x^2$ e limite superior $y=2$. Calcule os volumes quando rotacionamos essa região:
- Ao redor do eixo $x$.
- Ao redor do eixo $y$.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2}-6x+10,y=-x^{2}+6x-6$, ao redor do eixo $y.$
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2},y^{2}=x$, ao redor do eixo $x$.
Considere um cilindro com base de diâmetro $2R$ e altura também $2R$. Considere, inscrito neste cilindro, uma esfera de raio $R$ e um cone de base circular com diâmetro $2R$ e altura $2R$. Denote por $V_{cil}$, $V_{esf}$ e $V_{cone}$, respectivamente, os volumes desses sólidos.
- Verifique as relações $V_{esf}= \frac{2}{3}V_{cil}$ e $V_{cone}=\frac{1}{3}V_{cil}.$
- Calcule $V_{cil}$, $V_{esf}$ e $V_{cone}$ usando integrais. Explicite o método que está usando.
Utilize o método das cascas cilíndricas para calcular o volume de um cone circular reto de altura $h$ e base com raio $r$.
Podemos pensar no cone como a superfície de revolução obtida pela rotação de um segmento de reta. A reta em questão pode ser equacionada, por semelhança de triângulos, como
\[
\frac{y}{x}=\frac{h}{r}\text{ ou }y:=y\left( x\right) =\frac{h}{r}x\text{.}%
\]
O segmento de reta é determinado ao restringirmos $x\in\left[ 0,r\right]$. Observamos que, dado $x\in\left[ 0,r\right] $ temos que a altura $h\left( x\right) $ correspondente ao cilindro contido no cone é $h\left( x\right) =h-y\left( x\right) $. Chamando o volume de $V$, pelo método das cascas cilíndricas, obtemos que:
\begin{align*}
V & =\int_{0}^{r}\left( 2\pi x\right) \left( h-\frac{h}{r}x\right) dx\\
& =\int_{0}^{r}2\pi h\left( x-\frac{x^{2}}{r}\right) dx\\
& =2\pi h\left. \left( \frac{x^{2}}{2}-\frac{x^{3}}{3r}\right) \right\vert
_{0}^{r}\\
& =2\pi h\left( \frac{r^{2}}{2}-\frac{r^{3}}{3r}\right) \\
& =2\pi h\frac{r^{2}}{6}\\
& =\frac{\pi hr^{2}}{3}.
\end{align*}
Um projetista, incumbido da tarefa de projetar uma bacia com cerca de $3L$ de capacidade, resolveu fazê-la nos moldes de uma tampa de uma casca esférica de $r=16cm$, com $9cm$ de profundidade, conforme a figura abaixo. Calcule o volume da bacia projetada e veja se a estimativa do projetista foi adequada, dado que a margem de erro do volume estabelecida pela empresa era de $15\%$.
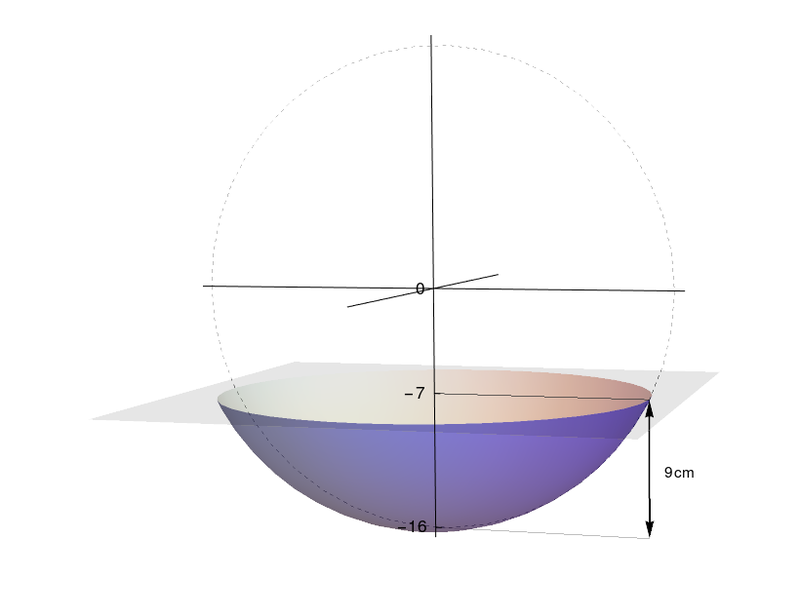
Podemos calcular o volume da bacia através da seguinte integral:
$V=\int_{7}^{16}\pi\left(\sqrt{16^2-x^2}\right)^2\,dx=\left.\left[\pi(256x-\frac{x^3}{3})\right]\right\vert_7^{16}=1053\pi$
Lembrando que $1L=1000cm^3$ e supondo $\pi\approx3$, temos $V=3159cm^3$ (O valor real é próximo de $V=3308cm^3$). Como a margem de erro do projetista era de $15\%$, vemos que este acertou em seus cálculos.
A região no plano $xy$ limitada pela curva $y=x^2+1$ e pela reta $y=-x+3$ gira em torno do eixo $x$ gerando um sólido $S.$ Calcule o volume de $S.$
Mostre que o volume de uma esfera de raio $R$ é $\dfrac{4}{3}\pi R^{3}$.
Usando a fórmula do volume de uma calota esférica, encontre o volume do sólido que sobra quando um buraco de raio $\dfrac{r}{2}$ é feito através do centro de uma esfera de raio $r$ e verifique a sua resposta por integração.
Encontre o volume do sólido obtido pela rotação da região limitada por $y=x-x^{2}$ e $y=0$ ao redor da reta $x=2$.
A região limitada pelo triângulo de vértices $(1,0),$ $(2,1)$ e $(1,1)$ gira em torno do eixo $y$ gerando um sólido $S.$ Calcule o volume de $S.$
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=e^{x},y=0,x=0,x=1$ ao redor do eixo $x.$
A cápsula cônica de reentrada de um veículo espacial é desenhada de tal forma que uma secção transversal tomada $x$ pés da ponta e perpendicular ao eixo de simetria é um círculo de raio $\dfrac{1}{4}x^2$ pés. Ache o volume do cone sabendo que o seu comporimento é de $20$ pés.
Seja $S$ a região entre as curvas $y=x^n$ e $y=x^{n+1}$, onde $n$ é um inteiro, $n\geq 1$.
Considere o sólido $A_r$ obtido pela rotação de $S$ ao redor do eixo $x=r, r>1$ e considere o sólido $B_r$ obtido pela rotação de $S$ ao redor do eixo $y=r, r>1$. \\
Calcule o volume $V(A_r)$ de $A_r$, o volume $V(B_r)$ de $B_r$. Determine, se existir, ${\lim_{r\rightarrow\infty}\frac{V(A_r)}{V(B_r)}}$.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=e^{-x^{2}},y=0,x=0,x=1$, ao redor do eixo $y.$
Ache o volume do sólido cuja base é a região limitada pelas curvas $y=x$ e $y=x^2$ cujas secções transversais perpendiculares ao eixo $x$ são quadrados.

