Rotacional e Divergente
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Determine se o campo vetorial $\mathbf{F}(x,y,z) = y^2z^3\mathbf{i} + 2xyz^3\mathbf{j} + 3xy^2z^2\mathbf{k}$ é conservativo ou não. Se for conservativo, determine uma função $f$ tal que $\mathbf{F} = \nabla{f}$.
$\mathbf{F}$ é conservativo. $f(x,y,z) = xy^2 z^3.$
A primeira identidade de Green é dada por:
$$\iint\limits_{ D} f\nabla^2g \, dA = \oint_{C}f(\nabla{g}) \cdot \mathbf{n} \, ds - \iint\limits_{ D}\nabla{f} \cdot \nabla{g} \, dA,$$
em que $D$ e $C$ satisfazem as hipóteses do Teorema de Green e as derivadas parciais apropriadas de $f$ e $g$ existem e são contínuas. (A quantidade $ \nabla{g} \cdot \mathbf{n} = D_{\mathbf{n}}g$ aparece na integral de linha. Essa é a derivada direcional na direção do vetor normal $\mathbf{n}$ e é chamada derivada normal de $g$.) Use-a para demonstrar a segunda identidade de Green:
$$\iint\limits_{ D} (f\nabla^2g - g\nabla^2f)\, dA = \oint_{C}(f\nabla{g} - g\nabla{f}) \cdot \mathbf{n} \, ds,$$
em que $D$ e $C$ satisfazem as hipóteses do Teorema de Green e as derivadas parciais apropriadas de $f$ e $g$ existem e são contínuas.
Note que pela primeira identidade de Green,
$$\iint\limits_{ D} (f\nabla^2g - g\nabla^2f)\, dA = \oint_{C}(f\nabla{g} \cdot \mathbf{n} - g\nabla{f} \cdot \mathbf{n}) \, ds, + \iint\limits_{ D} (\nabla f \cdot \nabla g - \nabla g \cdot \nabla f)\, dA.$$
Mostre que $f(x,y) = \ln{(x^2+y^2)}$ satisfaz a equação de Laplace $\nabla^2f = 0$, exceto no ponto $(0,0).$
Note que se $(x,y) \neq (0,0),$ $\nabla^2f = \dfrac{\partial}{\partial x} \left[ \dfrac{2x}{x^{2} + y^{2}} \right] + \dfrac{\partial}{\partial y} \left[ \dfrac{2y}{x^{2} + y^{2}} \right].$
Seja $f$ um campo escalar e $\mathbf{F}$ um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
$\text{rot }{f}$;
$\text{div }{\mathbf{F}}$;
$\text{grad }{\mathbf{F}}$.
$\text{rot }{f}$ não tem significado, pois $f$ é um campo escalar.
$\text{div }{\mathbf{F}}$ é um campo escalar.
$\text{grad }{\mathbf{F}}$ não tem sifnificado, pois $\bf{F}$ não é um campo escalar.
As equações de Maxwell relacionam o campo elétrico $\mathbf{E}$ e o campo magnético $\mathbf{H}$, quando eles variam com o tempo em uma região que não contenha carga nem corrente, como segue:
$$\text{div }{\mathbf{E}} = 0,\text{ }\text{div }{\mathbf{H}} = 0$$
$$\text{rot }{\mathbf{E}} = -\dfrac{1}{c}\dfrac{\partial\mathbf{H}}{\partial t},\text{ }\text{rot }{\mathbf{H}} = \dfrac{1}{c}\dfrac{\partial\mathbf{E}}{\partial t},$$
em que $c$ é a velocidade da luz. Use essas equações para demonstrar o seguinte:
$\nabla \times (\nabla \times \mathbf{E}) = - \dfrac{1}{c^2}\dfrac{\partial^2\mathbf{E}}{\partial t^2}$,
$\nabla \times (\nabla \times \mathbf{H}) = - \dfrac{1}{c^2}\dfrac{\partial^2\mathbf{H}}{\partial t^2}$,
$\nabla^2{\mathbf{E}} = \dfrac{1}{c^2}\dfrac{\partial^2\mathbf{E}}{\partial t^2}$,
$\nabla^2{\mathbf{H}} = \dfrac{1}{c^2}\dfrac{\partial^2\mathbf{H}}{\partial t^2}$.
$\nabla \times (\nabla \times \mathbf{E}) = \nabla \times (\text{rot } \mathbf{E}) = \nabla \times \left( -\dfrac{1}{c} \dfrac{\partial \mathbf{H}}{\partial t} \right) = -\dfrac{1}{c} \dfrac{\partial}{\partial t} \text{rot } \mathbf{H} = -\dfrac{1}{c} \dfrac{\partial}{\partial t} \left(\dfrac{1}{c} \dfrac{\partial \mathbf{E}}{\partial t} \right)$
Análogo ao item 1.
Note que $\nabla^2{\mathbf{E}} = \nabla \text{div } \mathbf{E} - \text{rot } \text{rot }(\mathbf{E}).$
Análogo ao item 3.
O campo vetorial $\mathbf{F}$ é mostrado no plano $xy$ e é o mesmo em todos os planos horizontais (em outras palavras, $\mathbf{F}$ é independente de $z$ e sua componente $z$ é 0).
O $\text{div }{\mathbf{F}}$ será positivo, negativo ou nulo? Justifique.
Determine se o $\text{rot }{\mathbf{F}} = 0$. Se não, em que direção rot $\mathbf{F}$ aponta?

Nulo.
$\text{rot } \bf{F}$ aponta na direção negativa do eixo $z.$
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = e^x\sin{y}\mathbf{i} + e^x\cos{y}\mathbf{j} + z\mathbf{k}$.
$\text{rot } \mathbf{F} = \bf{0}.$ $\text{div } \mathbf{F} = 1.$
Demonstre as identidades, admitindo que as derivadas parciais apropriadas existem e são contínuas. Se $f$ for um campo escalar e $\mathbf{F}$, $\mathbf{G}$ foram campos vetoriais, então $f\mathbf{F}$, $\mathbf{F} \cdot \mathbf{G}$ e $\mathbf{F} \times \mathbf{G}$ serão definidos por
$$\begin{array}{rcl}(f\mathbf{F})(x,y,z) & = & f(x,y,z)\mathbf{F}(x,y,z) \\(\mathbf{F} \cdot \mathbf{G})(x,y,z) & = & \mathbf{F}(x,y,z) \cdot \mathbf{G}(x,y,z) \\(\mathbf{F} \times \mathbf{G})(x,y,z) & = & \mathbf{F}(x,y,z) \times \mathbf{G}(x,y,z).\end{array}$$
$\text{div }{(\mathbf{F}+\mathbf{G})} = \text{div }{\mathbf{F}}+\text{div }{\mathbf{G}}$.
$\text{div }{(f\mathbf{F})} = f\text{div }{\mathbf{F}} + \mathbf{F} \cdot \nabla{f}$.
$\text{div }{(\mathbf{F} \times \mathbf{G})} = \mathbf{G} \cdot \text{rot }{\mathbf{F}} - \mathbf{F}\cdot\text{rot }{\mathbf{G}}$.
$\text{div }{(\nabla{f} \times \nabla{g})} = 0$.
Suponhamos que ${\bf F}=P_{1}\,{\bf i}+Q_{1}\,{\bf j}+R_{1}\,{\bf k}$ e ${\bf G}=P_{2}\,{\bf i}+Q_{2}\,{\bf j}+R_{2}\,{\bf k}.$
Temos que $F+G=(P_{1}+P_{2})\,{\bf i}+(Q_{1}+Q_{2})\,{\bf j}+(R_{1}+R_{2})\,{\bf k}$. Então,
$$\begin{array}{rcl}\text{div } ({\bf F}+{\bf G})&=&\frac{\partial(P_{1}+P_{2})}{\partial x}+\frac{\partial(Q_{1}+Q_{2})}{\partial y}+\frac{\partial(R_{1}+R_{2})}{\partial z}\\&=&\frac{\partial P_{1}}{\partial x}+\frac{\partial P_{2}}{\partial x}+\frac{\partial Q_{1}}{\partial y}+\frac{\partial Q_{2}}{\partial y}+\frac{\partial R_{1}}{\partial z}+\frac{\partial R_{2}}{\partial z}\\&=&\underbrace{\frac{\partial P_{1}}{\partial x}+\frac{\partial Q_{1}}{\partial y}+\frac{\partial R_{1}}{\partial z}}+\underbrace{\frac{\partial P_{2}}{\partial x}+\frac{\partial Q_{2}}{\partial y}+\frac{\partial R_{2}}{\partial z}}\\&=& \text{div } {\bf F} + \text{div }{\bf G}.\end{array}$$
Temos que $f{\bf F}=(fP_{1})\,{\bf i}+(fQ_{1})\,{\bf j}+(fR_{1})\,{\bf k}.$ Então,
$$\begin{array}{rcl}\text{div } (f{\bf F})&=&\frac{\partial(fP_{1})}{\partial x}+\frac{\partial(fQ_{1})}{\partial y}+\frac{\partial(fR_{1})}{\partial z}\\&=&\frac{\partial f}{\partial x}\cdot P_{1}+f\cdot\frac{\partial P_{1}}{\partial x}+\frac{\partial f}{\partial y}\cdot Q_{1}+f\cdot\frac{\partial Q_{1}}{\partial y}+\frac{\partial f}{\partial z}\cdot R_{1}+f\cdot \frac{\partial R_{1}}{\partial z}\\&=&f\cdot\bigg(\underbrace{\frac{\partial P_{1}}{\partial x}+\frac{\partial Q_{1}}{\partial y}+\frac{\partial R_{1}}{\partial z}}\bigg)+\underbrace{\frac{\partial f}{\partial x}P_{1}+\frac{\partial f}{\partial y}Q_{1}+\frac{\partial f}{\partial z}R_{1}}\\&=& f\cdot \text{div } {\bf F}+ \nabla f\cdot {\bf F}\end{array}$$
Temos que ${\bf F}\times {\bf G}=(Q_{1}R_{2}-Q_{2}R_{1})\,{\bf i}+(P_{2}R_{1}-P_{1}R_{2})\,{\bf j}+(P_{1}Q_{2}-Q_{1}R_{2})\,{\bf k}.$ Então,
$$\begin{array}{rcl}\text{div } ({\bf F}\times {\bf G})&=&\frac{\partial(Q_{1}R_{2}-Q_{2}R_{1})}{\partial x}+\frac{\partial(P_{2}R_{1}-P_{1}R_{2})}{\partial y}+\frac{\partial(P_{1}Q_{2}-P_{2}Q_{1})}{\partial z}\\&=&\frac{\partial (Q_{1}R_{2})}{\partial x}-\frac{\partial (Q_{2}R_{1})}{\partial x}+\frac{\partial (P_{2}R_{1})}{\partial y}-\frac{\partial (P_{1}R_{2})}{\partial y}+\frac{\partial (P_{1}Q_{2})}{\partial z}-\frac{\partial (Q_{1}R_{2})}{\partial z}\\&=&\frac{\partial Q_{1}}{\partial x}\cdot R_{2}+Q_{1}\cdot \frac{\partial R_{2}}{\partial x}-\frac{\partial Q_{2}}{\partial x}\cdot R_{1}-Q_{2}\cdot \frac{\partial R_{1}}{\partial x}+\frac{\partial P_{2}}{\partial y}\cdot R_{1}+P_{2}\cdot \frac{\partial R_{1}}{\partial y}\\&-&\frac{\partial P_{1}}{\partial y}\cdot R_{2}-P_{1}\cdot \frac{\partial R_{2}}{\partial y}+\frac{\partial P_{1}}{\partial z}\cdot Q_{2}+P_{1}\cdot \frac{\partial Q_{2}}{\partial z}-\frac{\partial P_{2}}{\partial z}-P_{2}\cdot \frac{\partial Q_{1}}{\partial z}\\&=&P_{1}\bigg(\frac{\partial Q_{2}}{\partial z}-\frac{\partial R_{2}}{\partial y}\bigg)+Q_{1}\bigg(\frac{\partial R_{2}}{\partial x}-\frac{\partial P_{2}}{\partial z}\bigg)+R_{1}\bigg(\frac{\partial P_{2}}{\partial y}-\frac{\partial Q_{2}}{\partial x}\bigg)\\&+&P_{2}\bigg(\frac{\partial R_{1}}{\partial y}-\frac{\partial Q_{1}}{\partial z}\bigg)+Q_{2}\bigg(\frac{\partial P_{1}}{\partial z}-\frac{\partial R_{1}}{\partial x}\bigg)+R_{2}\bigg(\frac{\partial Q_{1}}{\partial x}-\frac{\partial P_{1}}{\partial y}\bigg)\\&=&\bigg[-P_{1}\bigg(\frac{\partial R_{2}}{\partial y}-\frac{\partial Q_{2}}{\partial z}\bigg)-Q_{1}\bigg(\frac{\partial P_{2}}{\partial z}-\frac{\partial R_{2}}{\partial x}\bigg)-R_{1}\bigg(\frac{\partial Q_{2}}{\partial x}-\frac{\partial P_{2}}{\partial y}\bigg)\bigg]\\&+&\bigg[P_{2}\bigg(\frac{\partial R_{1}}{\partial y}-\frac{\partial Q_{1}}{\partial z}\bigg)+Q_{2}\bigg(\frac{\partial P_{1}}{\partial z}-\frac{\partial R_{1}}{\partial x}\bigg)+R_{2}\bigg(\frac{\partial Q_{1}}{\partial x}-\frac{\partial P_{1}}{\partial y}\bigg)\bigg]\\&=&-{\bf F}\cdot \text{rot } {\bf G}+{\bf G}\cdot \text{rot } {\bf F}\\&=&{\bf G}\cdot \text{rot } {\bf F}-{\bf F}\cdot \text{rot } {\bf G}.\end{array}$$
Do item anterior temos que
$$\begin{array}{rcl}\text{div }(\nabla f\times \nabla g)&=&\nabla g \cdot \text{rot } (\nabla f)-\nabla f \cdot \text{rot } (\nabla g).\\\end{array} $$
Sabemos que, se $f$ é uma função de três variáveis que tem derivadas parciais de segunda ordem contínuas, então $\text{rot } (\nabla f)={\bf 0}.$ Deste resultado, obtemos que
$$\text{div }(\nabla f\times \nabla g) =\nabla g \cdot {\bf 0}-\nabla f \cdot {\bf 0}=0.$$
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário), onde $\mathbf{F}(x,y) = y\mathbf{j}$, $C$ a fronteira do quadrado de vértices $(0,0)$, $(1,0)$, $(1,1)$, $(0,1)$ e $\mathbf{n}$ a normal que aponta para fora do quadrado, sendo $C$ orientada no sentido anti-horário.
$1.$
Seja $f$ um campo escalar e $\mathbf{F}$ um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
$\text{grad }{f}$;
$\text{rot }{(\text{grad }{f})}$;
$\text{grad }{(\text{div }{\mathbf{F}})}$.
$\text{grad }{f}$ é um campo gradiente.
$\text{rot }{(\text{grad }{f})}$ é um campo vetorial.
$\text{grad }{(\text{div }{\mathbf{F}})}$ é um campo vetorial.
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla^2r^3=12r$.
$\nabla^2r^3= \dfrac{\partial}{\partial x} \left[ \dfrac{3}{2} \sqrt{x^{2} + y^{2} + z^{2}} (2x) \right] + \dfrac{\partial}{\partial y} \left[ \dfrac{3}{2} \sqrt{x^{2} + y^{2} + z^{2}} (2y) \right]\\ + \dfrac{\partial}{\partial z} \left[ \dfrac{3}{2} \sqrt{x^{2} + y^{2} + z^{2}} (2z) \right].$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Determine se o campo vetorial $\mathbf{F}(x,y,z) = ye^{-x}\mathbf{i} + e^{-x}\mathbf{j} + 2z\mathbf{k}$ é conservativo ou não. Se for conservativo, determine uma função $f$ tal que $\mathbf{F} = \nabla{f}$.
$\mathbf{F}$ não é conservativo.
Seja
$$\mathbf{F}(x,y) = \dfrac{x}{(x^2+y^2)^5}\mathbf{i} + \dfrac{y}{(x^2+y^2)^5}\mathbf{j}$$
e $\mathbf{n}$ a normal unitária exterior ao círculo $x^2 + y^2 \leq 1$. Calcule $\int_{C} \mathbf{F} \cdot \mathbf{n} \, ds$, em que $C$ é dada por $\mathbf{r}(t) = (\cos{t},\sin{t})$, $0 \leq t \leq \pi$. (Sugestão: Verifique que $\mathbf{F} \cdot \mathbf{n}$ é constante.)
$\pi.$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla\left(\dfrac{1}{r}\right) = -\dfrac{\mathbf{r}}{r^3}$.
$\nabla\left(\dfrac{1}{r}\right) =- \dfrac{\frac{1}{2\sqrt{x^2 + y^2 + z^2}} (2x)}{x^2 + y^2 + z^2} \mathbf{i} - \dfrac{-\frac{1}{2\sqrt{x^2 + y^2 + z^2}} (2y)}{x^2 + y^2 + z^2} \mathbf{j} - \dfrac{-\frac{1}{2\sqrt{x^2 + y^2 + z^2}} (2z)}{x^2 + y^2 + z^2} \mathbf{k}.$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Determine se o campo vetorial $\mathbf{F}(x,y,z) = 2xy\mathbf{i} + (x^2+2yz)\mathbf{j} + y^2\mathbf{k}$ é conservativo ou não. Se for conservativo, determine uma função $f$ tal que $\mathbf{F} = \nabla{f}$.
$\mathbf{F}$ é conservativo. $f(x,y,z) = x^2 y + y^2 z.$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla{\ln{r}} = \dfrac{\mathbf{r}}{r^2}$.
$\nabla{\ln{r}} = \dfrac{1}{2} \nabla \ln (x^{2} + y^{2} + z^{2}).$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = (\ln{x},\ln{(xy)},\ln{(xyz)})$.
$\text{rot } \mathbf{F} = \dfrac{1}{y}\mathbf{i} - \dfrac{1}{x} \mathbf{j} +\dfrac{1}{x} \mathbf{k}.$ $\text{div } \mathbf{F} = \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}.$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla \cdot \mathbf{r} = 3$.
$\nabla \cdot \mathbf{r} = \left(\dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right) \cdot \left(x,y,z \right)$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla{r} = \dfrac{\mathbf{r}}{r}$.
$\nabla{r} = \left(\dfrac{x}{\sqrt{x^2 + y^2 + z^2}},\dfrac{y}{\sqrt{x^2 + y^2 + z^2}} ,\dfrac{z}{\sqrt{x^2 + y^2 + z^2}} \right).$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Use o Teorema de Green na forma $\oint_{C} \mathbf{F} \cdot \mathbf{n} \, ds = \iint\limits_{ D} \text{div }{\mathbf{F}(x,y)} \, dA$ para demonstrar a primeira identidade de Green:
$$\iint\limits_{ D} f\nabla^2g \, dA = \oint_{C}f(\nabla{g}) \cdot \mathbf{n} \, ds - \iint\limits_{ D}\nabla{f} \cdot \nabla{g} \, dA,$$
em que $D$ e $C$ satisfazem as hipóteses do Teorema de Green e as derivadas parciais apropriadas de $f$ e $g$ existem e são contínuas. (A quantidade $ \nabla{g} \cdot \mathbf{n} = D_{\mathbf{n}}g$ aparece na integral de linha. Essa é a derivada direcional na direção do vetor normal $\mathbf{n}$ e é chamada derivada normal de $g$.)
Note que $\oint_{C} f(\nabla{g}) \cdot \mathbf{n} \, ds = \iint\limits_{ D} \text{div }(f \nabla g) \, dA = \iint\limits_{ D} f\text{div }(\nabla g) + \nabla{f} \cdot \nabla{g} \, dA.$
Determine se o campo vetorial $\mathbf{F}(x,y,z) = y\cos{xy}\mathbf{i} + x\cos{xy}\mathbf{j} - \sin{z}\mathbf{k}$ é conservativo ou não. Se for conservativo, determine uma função $f$ tal que $\mathbf{F} = \nabla{f}$.
$\mathbf{F}$ é conservativo. $f(x,y,z) = \sin(xy) + \cos(z).$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla \times \mathbf{r} = \mathbf{0}$.
$\nabla \times \mathbf{r} = \left[\dfrac{\partial}{\partial y} (z) - \dfrac{\partial}{\partial z}(y) \right]\mathbf{i} + \left[\dfrac{\partial}{\partial z} (x) - \dfrac{\partial}{\partial x}(z) \right]\mathbf{j} + \left[\dfrac{\partial}{\partial x} (y) - \dfrac{\partial}{\partial y}(x) \right]\mathbf{k}.$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
O campo vetorial $\mathbf{F}$ é mostrado no plano $xy$ e é o mesmo em todos os planos horizontais (em outras palavras, $\mathbf{F}$ é independente de $z$ e sua componente $z$ é 0).
O $\text{div }{\mathbf{F}}$ será positivo, negativo ou nulo? Justifique.
Determine se o $\text{rot }{\mathbf{F}} = 0$. Se não, em que direção rot $\mathbf{F}$ aponta?
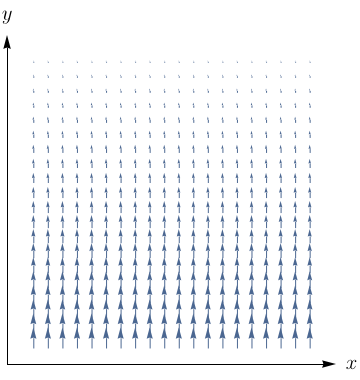
Negativo.
$\text{rot } \bf{F} = \bf{0}.$
Considerando um campo vetorial $\mathbf{F}$ que representa a velocidade em um fluido, a interpretação do rotacional é que partículas em um ponto $(x,y,z)$ de um fluido tendem a rodar em torno do eixo que aponta na direção de $\text{rot }\mathbf{F}(x,y,z)$. Se $\mathbf{F}$ representar a velocidade da corrente de um rio calmo, que corre somente da direção montante à jusante, podemos dizer que $\text{rot } \mathbf{F}$ é igual ou diferente de zero? Por quê? Para auxiliar na interpretação, faça um esboço do gráfico de $\mathbf{F}$ assumindo que ele não varia na direção $z$.
Igual a zero.
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário), onde $\mathbf{F}(x,y) = x\mathbf{i} + y\mathbf{j}$, $C$ dada por $\mathbf{r}(t) = (t,t^2)$, $0 \leq t \leq 1$ e $\mathbf{n}$ a normal com componente $y < 0$.
$\dfrac{1}{3}$.
Mostre que qualquer campo vetorial da forma
$$\mathbf{F}(x,y,z) = f(y,z)\mathbf{i} + g(x,z)\mathbf{j} + h(x,y)\mathbf{k}$$
é incompressível.
Note que $\text{div } \mathbf{F} = 0.$
Seja $f$ um campo escalar e $\mathbf{F}$ um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
$\text{div }{(\text{grad }{f})}$;
$\text{rot }{(\text{rot }{\mathbf{F}})}$;
$(\text{grad }{f}) \times (\text{div }{\mathbf{F}})$.
$\text{div }{(\text{grad }{f})}$ é um campo escalar.
$\text{rot }{(\text{rot }{\mathbf{F}})}$ é um campo vetorial.
$(\text{grad }{f}) \times (\text{div }{\mathbf{F}})$ não tem significado pois $\text{div } \bf{F}$ é um campo escalar.
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário), onde $\mathbf{F}(x,y) = x^2\mathbf{i}$, $C$ dada por $\mathbf{r}(t) = (2\cos{t},\sin{t})$, $0 \leq t \leq 2\pi$ e $\mathbf{n}$ a normal que aponta para fora da região $x^2/4+y^2\leq 1$.
$0$.
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário), onde $\mathbf{F}(x,y) = x^2\mathbf{i}$, $C$ dada por $\mathbf{r}(t) = (2\cos{t},\sin{t})$, $0 \leq t \leq \pi$ e $\mathbf{n}$ a normal com componente $y \geq 0$.
$0$.
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla \cdot (r\mathbf{r}) = 4r$.
$\nabla \cdot (r\mathbf{r}) = \left( \dfrac{x^{2}}{\sqrt{x^{2} + y^{2} + z^{2}}} + \sqrt{x^{2} + y^{2} + z^{2}} \right) + \left( \dfrac{x^{2}}{\sqrt{y^{2} + y^{2} + z^{2}}} + \sqrt{y^{2} + y^{2} + z^{2}} \right)\\ + \left( \dfrac{z^{2}}{\sqrt{x^{2} + y^{2} + z^{2}}} + \sqrt{x^{2} + y^{2} + z^{2}} \right)$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
O campo vetorial $\mathbf{F}$ é mostrado no plano $xy$ e é o mesmo em todos os planos horizontais (em outras palavras, $\mathbf{F}$ é independente de $z$ e sua componente $z$ é 0).
O $\text{div }{\mathbf{F}}$ será positivo, negativo ou nulo? Justifique.
Determine se o $\text{rot }{\mathbf{F}} = 0$. Se não, em que direção rot $\mathbf{F}$ aponta?
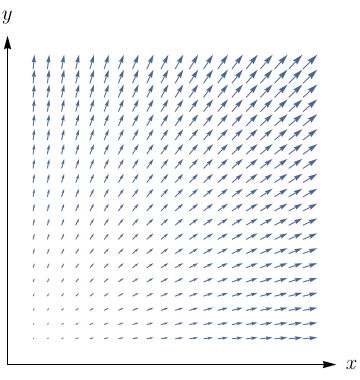
Positivo.
$\text{rot } \bf{F} = \bf{0}.$
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = xyz\mathbf{i} - x^2y\mathbf{k}$.
$\text{rot } \mathbf{F} = -x^2 \mathbf{i} + 3xy \mathbf{j} -xz \mathbf{k}.$ $\text{div } \mathbf{F} = yz.$
Seja $f$ um campo escalar e $\mathbf{F}$ um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
$\text{grad }{(\text{div }{f})}$;
$\text{div }{(\text{div }{\mathbf{F}})}$;
$\text{div }{(\text{rot }{(\text{grad }{f})})}$.
$\text{grad }{(\text{div }{f})}$ não tem significado, pois $f$ é um campo escalar.
$\text{div }{(\text{div }{\mathbf{F}})}$ não tem significado pois $\text{div } \bf{F}$ é um campo escalar.
$\text{div }{(\text{rot }{(\text{grad }{f})})}$ é um campo escalar.
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = e^{xy}\sin{z}\mathbf{j} + y\tan^{-1}(x/z)\mathbf{k}$.
$\text{rot } \mathbf{F} = (\arctan(x/z) - e^{xy}\cos(z))\mathbf{i} - \dfrac{yz}{x^{2} + z^{2}} \mathbf{j} + ye^{xy}\sin(z) \mathbf{k}.$ $\text{div } \mathbf{F} = xe^{xy}\sin(z) - \dfrac{xy}{x^{2} + z^{2}}.$
Existe um campo vetorial $\bf{G}$ em $\mathbb{R}^3$ tal que $\text{rot }{\bf{G}} = (x\sin{y},\cos{y},z-xy)$? Justifique.
Suponha que existe um campo vetorial $\bf G$ tal que $\text{rot } G= (x\,\sin y, \cos y,z-xy)$. Vamos calcular $\text{div } \text{rot } {\bf G}.$
Temos que
$$\text{div } \text{rot } {\bf G}=\frac{\partial (x\,\sin y) }{\partial x}+\frac{\partial (\cos{y})}{\partial y}+\frac{\partial (z-xy)}{\partial z}$$
$$=\sin y- \sin y +1=1.$$
Sabemos que se ${\bf F}=P\,{\bf i}+Q\,{\bf j}+R\,{\bf k}$ é um campo vetorial sobre $\mathbb{R}^{3}$ e $P$, $Q$ e $R$ têm derivadas parciais de segunda ordem contínuas, então $\text{div } \text{rot } {\bf F}=0.$
Como $\text{div } \text{rot } {\bf G}\neq 0$, pela contrapositiva do resultado acima, temos que ${\bf G}$ não é um campo vetorial do $\mathbb{R}^{3}.$
Prove que se $\mathbf{F} \cdot \mathbf{n}$ for constante sobre $Im\,\mathbf{r}$, então o fluxo de $\mathbf{F}$ sobre $\mathbf{r}$ é o produto de $\mathbf{F} \cdot \mathbf{n}$ pelo comprimento de $\mathbf{r}$, em que $\mathbf{n}$ é normal a $\mathbf{r}$.
Direto da definição do fluxo de $\mathbf{F}$ através de $\bf{r}$ na direção $\bf{n}.$
Mostre que qualquer campo vetorial da forma
$$\mathbf{F}(x,y,z) = f(x)\mathbf{i} + g(y)\mathbf{j} + h(z)\mathbf{k},$$
em que $f,g$ e $h$ são diferenciáveis, é irrotacional.
Note que $\text{rot } \mathbf{F} = \bf{0}.$
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = \dfrac{1}{\sqrt{x^2+y^2+z^2}}(x\mathbf{i} + y\mathbf{j} + z\mathbf{k})$.
$\text{rot } \mathbf{F} = \bf{0}.$ $\text{div } \mathbf{F} = \dfrac{2}{\sqrt{x^{2} + y^{2} + z^{2}}}.$
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário, onde $\mathbf{F}(x,y) = x\mathbf{i} + y\mathbf{j}$, $C$ dada por $\mathbf{r}(t) = (\cos{t},\sin{t})$, $0 \leq t \leq 2\pi$ e $\mathbf{n}$ a normal exterior.
$2\pi.$

