LISTA DE DISCIPLINAS

| MA211 - Cálculo II | Integrais triplas

Integrais triplas

Selecione os exercícios por

Dificuldade

Categoria

Outros

Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.

2534   

Determine a massa e o centro de massa do cubo dado por $0\leq x\leq a$, $0\leq y\leq a$, $0\leq z\leq a$ e com função densidade:

  1.  $\rho(x,y,z)=x^{2}+y^{2}+z^{2}.$

  2.  $\rho(x,y,z)=x+y+z.$

  1.  Massa: $a^5;$ centro de massa: $\displaystyle \left(\frac{7a}{12},\frac{7a}{12},\frac{7a}{12} \right).$

  2.  Massa: $\dfrac{3a^4}{2};$ centro de massa: $\displaystyle \left(\frac{5a}{9},\frac{5a}{9},\frac{5a}{9} \right).$

2496   

Para qual valor de $c$ o volume do elipsóide $x^{2}+(y/2)^{2}+(z/c)^{2}=1$ é igual a $8\pi$?

$3.$

3050   

A figura mostra a região de integração da integral

$$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx.$$

Reescreva essa integral como uma integral iterada equivalente nas cinco outras ordens.

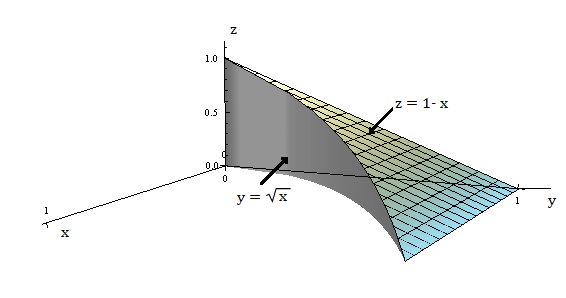
ma211lista8q15.png

$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx = \int_{0}^{1}\int_{0}^{y^2}\int_{0}^{1-y}f(x,y,z)\;dz dx dy $
$= \int_{0}^{1}\int_{0}^{1 - z}\int_{0}^{y^2}f(x,y,z)\;dx dy dz = \int_{0}^{1}\int_{0}^{1 - y}\int_{0}^{y^2}f(x,y,z)\;dx dz dy $
$= \int_{0}^{1}\int_{0}^{1 - \sqrt{x}}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dz dx = \int_{0}^{1}\int_{0}^{(1 - z)^2}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dx dz.$

3115   

Seja \(G\) a caixa retangular definida pelas desigualdades \(a\leq x\leq b\),  \(c\leq y\leq d\) e \(k\leq z\leq l\). Mostre que \[\iiint\limits_G f(x)g(y)h(z)\,dV = \left[\int_a^bf(x)\,dx\right]\left[\int_c^dg(y)\,dy\right]\left[\int_k^lh(z)\,dz\right].\]

2429   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E}x\;dx dy dz$, onde $E$ é o conjunto $0\leq x \leq 1$, $0\leq y \leq 1$ e \\ $x+y\leq z \leq x+y+1.$

  2.  $\displaystyle\iiint\limits_{  E}\sqrt{1-z^{2}}\;dx dy dz$, onde $E$ é o conjunto $0 \leq x \leq 1$, $0\leq z\leq 1$ e $0\leq y \leq z.$

  1.  $\dfrac{1}{2}.$

  2.  $\dfrac{1}{3}.$

2535   

Ache o centro de massa de $E$, em que:

  1.  A densidade de um ponto $P$ de um sólido cúbico $E$ de aresta $a$ é diretamente proporcional ao quadrado da distância de $P$ a um vértice fixo do cubo.

  2.  $E$ é o tetraedro delimitado pelos planos coordenados e o plano  $2x+5y+z=10$ e a densidade em $P(x,y,z)$ é diretamente proporcional $\grave{a}$ distância do plano $xz$ a $P.$

  1.  $\displaystyle \left( \dfrac{7a}{12},\dfrac{7a}{12},\dfrac{7a}{12} \right).$

  2.  $\displaystyle \left( 1,\dfrac{4}{5},2 \right).$

3056   

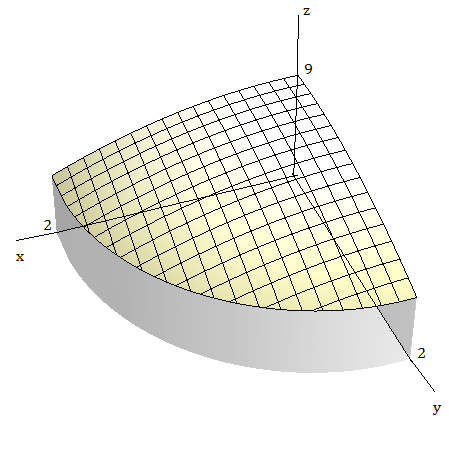
 Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral.

$\displaystyle \int_0^{\pi/2}\int_0^2\!\!\int_0^{9 - r^2} r dz dr d\theta$

ma211lista8q32bres.png

2484   

Use a integral tripla para determinar o volume do sólido dado.

  1.  $x^{2}\leq z \leq 1-y$ e $y\geq 0.$

  2.  $x^{2}+2y^{2}\leq z\leq 2a^{2}-x^{2}$ $(a>0).$

  3.  $x^{2}+y^{2}+(z-1)^{2}\leq 1$ e $z\geq x^{2}+y^{2}.$

  4.  $4x^{2}+9y^{2}+z^{2}\leq 4$ e $4x^{2}+9y^{2}\leq 1.$

  1.  $\dfrac{4}{15}.$

  2.  $\pi a^4.$

  3.  $\dfrac{71\pi}{54}.$

  4.  $\dfrac{7\pi}{12}.$

2430   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E}\sqrt{1-z^{2}}\;dx dy dz$, onde $E$ é o cubo $0\leq x\leq 1$, $0\leq y\leq 1$ e $0\leq z\leq 1.$

  2.  $\displaystyle\iiint\limits_{  E}\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq z \leq 2x.$

  1.  $\dfrac{\pi}{4}.$

  2.  $\dfrac{\pi}{2}.$

3055   

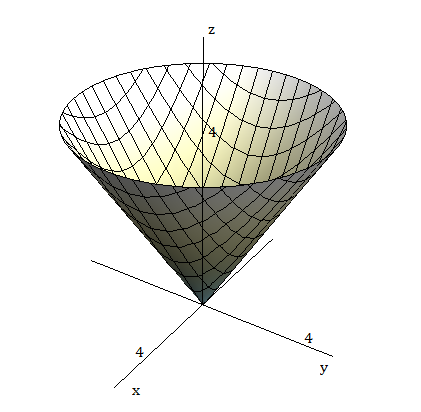
 Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral.

$\displaystyle \int_0^4 \int_0^{2\pi}\int_r^4 r \, dz d\theta dr$

ma211lista8q32ares.png

3051   

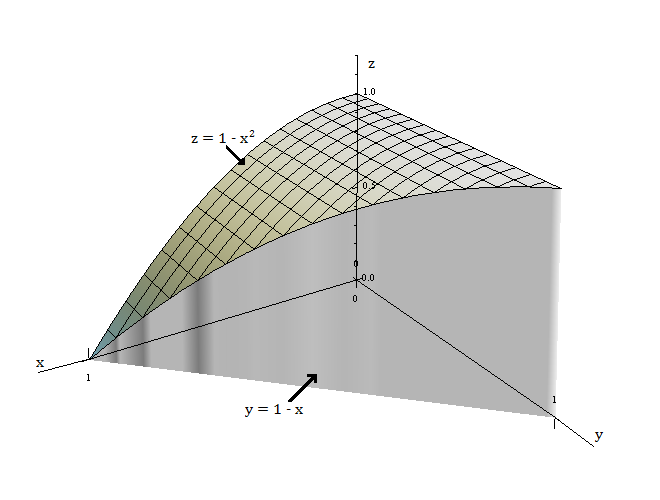
A figura mostra a região da integral

$$\int_{0}^{1}\int_{0}^{1-x^{2}}\int_{0}^{1-x}f(x,y,z)\;dy dz dx.$$

Reescreva essa integral como uma integral iterada equivalente nas cinco outras ordens.

ma211lista8q16.png

$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx = \int_{0}^{1}\int_{0}^{y^2}\int_{0}^{1-y}f(x,y,z)\;dz dx dy $
$= \int_{0}^{1}\int_{0}^{1 - z}\int_{0}^{y^2}f(x,y,z)\;dx dy dz = \int_{0}^{1}\int_{0}^{1 - y}\int_{0}^{y^2}f(x,y,z)\;dx dz dy $
$= \int_{0}^{1}\int_{0}^{1 - \sqrt{x}}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dz dx = \int_{0}^{1}\int_{0}^{(1 - z)^2}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dx dz.$

2454   

Calcule as integrais mudando a ordem de integração de maneira apropriada.

  1.  $\displaystyle\int_{0}^{4}\int_{0}^{1}\int_{2y}^{2}\dfrac{4\;\cos(x^{2})}{2\sqrt{z}}\;dx dy dz$

  2.    $\displaystyle\int_{0}^{1}\int_{0}^{1}\int_{x^{2}}^{1}12xze^{zy^{2}}\;dy dx dz$

  3.  $\displaystyle\int_{0}^{1}\int_{\sqrt[3]{z}}^{1}\int_{0}^{\ln 3}\dfrac{\pi e^{2x}\;\sin(\pi y^{2})}{y^{2}}\;dx dy dz$

  1.  $2 \sin(4).$

  2.  $3e - 6.$

  3.  $4.$

2421   

Calcule a integral tripla $\displaystyle\iiint\limits_{B}xyz^{2}\,dV$, onde $B$ é a caixa retangular dada por $B=\{(x,y,z) \in \mathbb{R}^3|\;0\leq x\leq 1,\;-1\leq y\leq 2,\;0\leq z\leq 3\}$, integrando primeiro em relação a $y$, depois a $z$ e então a $x$.

$\dfrac{27}{4}.$

3054   

Esboce o sólido cujo volume é dado pela integral iterada.

$\displaystyle\int_{0}^{2}\int_{0}^{2-y}\int_{0}^{4-y^{2}}\;dx dz dy$


ma211lista8q12bres.png

2539   

Encontre o centróide e os momentos de inércia $I_{x}$, $I_{y}$ e $I_{z}$ do tetraedro cujos vértices são os pontos $(0,0,0)$, $(1,0,0)$, $(0,1,0)$ e $(0,0,1).$

Centróide: $\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4} \right),$ $I_{x} = I_{y} = I_{z} = \dfrac{1}{30}.$

2455   

Encontre a constante $a$ tal que $$\int_{0}^{1}\int_{0}^{4-a-x^{2}}\int_{a}^{4-x^{2}-y}\;dz dy dx=\frac{4}{15}.$$

$\dfrac{13}{3}$ ou $3.$

2483   

Use a integral tripla para determinar o volume do sólido dado.

  1.  $x^{2}+y^{2}\leq 1$ e $x^{2}+z^{2}\leq 1.$

  2.  $(x-a)^{2}+y^{2}\leq a^{2}$, $x^{2}+y^{2}+z^{2}\leq 4a^{2}$, $z\geq 0$ $(a>0).$

  3.  $x^{2}+y^{2}\leq a^{2}$ e $x^{2}+z^{2}\leq a^{2}$ $(a>0).$

  4.  $x^{2}+y^{2}+z^{2}\leq a^{2}$ e $z\geq \dfrac{a}{2}$ $(a>0).$

  1.  $\dfrac{16}{3}.$

  2.  $\dfrac{16a^3}{3} \left(\dfrac{\pi}{2} - \dfrac{2}{3}\right).$

  3.  $\dfrac{16a^3}{3}.$

  4.  $\dfrac{5\pi a^3}{24}.$

2538   

Determine o sólido $E$ para o qual a integral $$ \iiint\limits_{  E}(1-x^{2}-2y^{2}-3z^{2})\,dV$$ é máxima.

$E = \left\{ (x,y,z);  x^2 + 2y^2 + 3z^2 \leq 1 \right\}.$

2426   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E}2x\,dV$, onde $E=\{(x,y,z)|\;0\leq y\leq 2,\,0\leq x\leq \sqrt{4-y^{2}},\;\\ 0\leq z\leq y\}.$

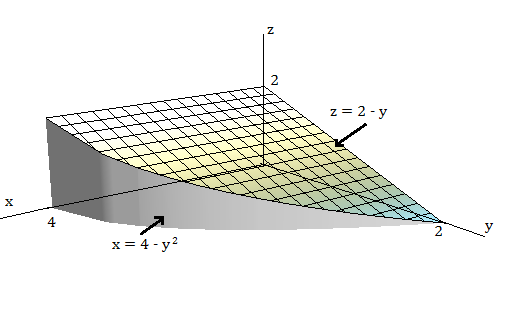
  2.  $\displaystyle\iiint\limits_{  E}6xy\,dV$, onde $E$ está abaixo do plano $z=1+x+y$ e acima da região do plano $xy$ limitada pelas curvas $y=\sqrt{x}$, $y=0$ e $x=1.$

  1.  $4.$

  2.  $\dfrac{65}{28}.$

2435   

Calcule a integral tripla.

  1. $\displaystyle\iiint\limits_{  E}2z\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$

  2. $\displaystyle\iiint\limits_{  E}2z\;dx dy dz$, onde $E$ é o conjunto $4x^{2}+9y^{2}+z^{2}\leq 4$ e $z\geq 0.$

  1.  $8\pi.$

  2.  $0.$

2536   

Calcule a massa do sólido $x+y+z\leq 1$, $x\geq 0$, $y\geq 0$ e $z\geq 0$, sendo a densidade dada por $\rho(x,y,z)=x+y.$

$\dfrac{1}{12}.$

2485   

Use a integral tripla para determinar o volume do sólido dado.

  1.  O tetraedro limitado pelos planos coordenados e o plano $2x+y+z=4.$

  2.  O sólido limitado pelo paraboloide $x=y^{2}+z^{2}$ e pelo plano $x=16.$

  3.  O sólido delimitado pelo cilindro $x=y^{2}$ e pelos planos $z=0$ e $x+z=1$.

  1.  $\dfrac{16}{3}.$

  2.  $128\pi.$

  3.  $\dfrac{8}{15}.$

2497   

Esboce o sólido cujo volume é dado pela integral iterada.

  1.  $\displaystyle\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{2-2z}\;dy dz dx$

  2.  $\displaystyle\int_{0}^{2}\int_{0}^{2-y}\int_{0}^{4-y^{2}}\;dx dz dy$

  3.  $\displaystyle\int_{0}^{1}\int_{\sqrt{1-z}}^{\sqrt{4-z}}\int_{2}^{3}\;dx dy dz$

  4.  $\displaystyle\int_{0}^{2}\int_{x^{2}}^{2x}\int_{0}^{x+y}\;dz dy dx$

  1. (... fig)

  2. (... fig.)

  3.  $\displaystyle \left\lbrace (x,y,z); 2 \leq x \leq 3,  \sqrt{1 - z} \leq y \leq \sqrt{4 - z} , 0 \leq z \leq 1\right\rbrace.$

  4.  $\displaystyle \left\lbrace (x,y,z); 0 \leq x \leq 2,  x^{2} \leq y \leq 2x , 0 \leq z \leq x + y\right\rbrace.$

2482   

Use a integral tripla para determinar o volume do sólido dado.

  1.  $x^{2}+y^{2}\leq 4$ e $x^{2}+y^{2}+z^{2}\leq 9.$

  2.  $x^{2}+4y^{2}+9z^{2}\leq 1.$

  3.  $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}$,  $(a>0,\;b>0\;e\;c>0).$

  4.  $x^{2}+y^{2}\leq z \leq 4x+2y.$

  1.  $\left(36 - \dfrac{20\sqrt{5}}{3} \right)\pi.$

  2.  $\dfrac{2\pi}{9}.$

  3.  $\dfrac{4\pi abc}{3}.$

  4.  $\dfrac{25\pi}{4}$

2431   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E}(x^{2}+z^{2})\;dx dy dz$, onde $E$ é o cilindro $x^{2}+y^{2}\leq 1$ e $0\leq z \leq 1.$

  2.  $\displaystyle\iiint\limits_{  E}\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq z \leq 2x+2y-1.$

  1.  $\dfrac{7\pi}{12}.$

  2.  $\dfrac{\pi}{2}.$

2427   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E} x^2 e^y\,dV$, onde $E$ é delimitado pelo cilindro parabólico $z=1-y^{2}$ e pelos planos $z=0$, $x=1$ e $x=-1.$

  2.  $\displaystyle\iiint\limits_{  E}x\,dV$, onde $E$ é limitado pelo paraboloide $x=4y^{2}+4z^{2}$ e  pelo plano $x=4.$

  1.  $\dfrac{8}{3e}.$

  2.  $\dfrac{16\pi}{3}.$

2432   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E}y\;dx dy dz$, onde $E$ é o conjunto $x^{2}+4y^{2}\leq 1$ e $0\leq z \leq 1.$

  2.  $\displaystyle\iiint\limits_{  E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq 4$, $x\geq 0$ e \\ $x+y\leq z \leq x+y+1.$

  1.  $0.$

  2.  $\dfrac{16}{3}.$

2420   

Use a integral tripla para determinar o volume do sólido dado por $x^{2}+y^{2}\leq z\leq \sqrt{4-3x^{2}-3y^{2}}.$


Primeiramente, vamos determinar a projeção no plano $xy$ da interseção de \begin{eqnarray*} z&=&\sqrt{4-3x^{2}-3y^{2}}\\ z&=&x^{2}+y^{2}. \end{eqnarray*} Da primeira equação temos que \begin{eqnarray*} \label{1}z=\sqrt{4-3x^{2}-3y^{2}}\Leftrightarrow z^{2}=4-3x^{2}-3y^{2}\Leftrightarrow z^{2}=4-3(x^{2}+y^{2}). \end{eqnarray*} Substituindo a segunda equação  na primeira, obtemos que $$z^{2}=4-z\Leftrightarrow z^{2}+3z-4=0\Leftrightarrow (z-1)(z-4)=0.$$ Logo, $z=-4$ e $z=1.$ Notemos que $z=-4$ não satisfaz as duas primeiras equações acima, então a projeção $D$ no plano $xy$ é o círculo de raio 1, isto é, $D=\{(x,y)\in \mathbb{R};\;\, x^{2}+y^{2}\leq 1\}.$ Assim, o volume, $V$, do sólido é: $$V=\iint\limits_{D}\bigg[\int_{x^{2}+y^{2}}^{\sqrt{4-3x^{2}-3y^{2}}}1\, dz\bigg]\,dA = \iint\limits_{ D}\sqrt{4-3x^{2}-3y^{2}}-(x^{2}+y^{2})\,dA.$$ Passando para coordenadas polares temos que \begin{eqnarray*}  x=r\cos \theta\\ y=r\sin \theta\\ dA=r\,dr\,d\theta\\ 0\leq r\leq 1\\ 0\leq \theta \leq 2\pi.\\ \end{eqnarray*} Então, $$V=\int_{0}^{2\pi}\int_{0}^{1}(\sqrt{4-3r^{2}}-r^{2})r\,dr\,d \theta=\int_{0}^{2\pi}\int_{0}^{1}(r\sqrt{4-3r^{2}}-r^{3})\,dr\,d\theta$$ $$=\int_{0}^{2\pi}\,d\theta\cdot \bigg[\bigg(\underbrace{\int_{0}^{1}r\sqrt{4-3r^{2}}\,dr}_{\substack{ u=4-3r^{2}\\ du=-6r\,dr}}\bigg)-\bigg(\int_{0}^{1}r^{3}\,dr\bigg)\bigg]$$ $$=\theta\bigg|_{0}^{2\pi}\cdot \bigg[\bigg(\int_{4}^{1}r\cdot u^{1/2}\frac{du}{-6r}\bigg)-\bigg(\frac{r^{4}}{4}\bigg|_{0}^{1}\bigg)\bigg]$$ $$=2\pi\cdot \bigg[\bigg(-\frac{1}{6}\int_{4}^{1}u^{1/2}\,du\bigg)-\frac{1}{4}\bigg]=2\pi \cdot \bigg[\bigg(-\frac{1}{6}\cdot \frac{2}{3}u^{3/2}\bigg|_{4}^{1}\bigg)-\frac{1}{4}\bigg]$$ $$=2\pi \cdot \bigg[-\frac{1}{9}+\frac{1}{9}\cdot 8-\frac{1}{4}\bigg]=2\pi \cdot \frac{19}{36}=\frac{19\pi}{18}.$$

2434   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E}e^{x^{2}}\;dx dy dz$, onde $E$ é o conjunto $0\leq x \leq 1$, $0\leq y \leq x$ e $0\leq z \leq 1.$

  2.  $\displaystyle\iiint\limits_{  E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}\leq y\leq x$, $0\leq z\leq x+y.$

  1.  $\dfrac{e - 1}{2}.$

  2.  $\dfrac{11}{120}.$

2433   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E}2z\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq 1$, $x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$

  2.  $\displaystyle\iiint\limits_{  E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}-y^{2}\leq z \leq 1-2y^{2}.$

  1.  $\dfrac{7\pi}{2}.$

  2.  $0.$

2422   

Calcule a integral iterada.

  1.  $\displaystyle\int_{0}^{1}\!\!\int_{0}^{z}\!\!\int_{0}^{x+z}6xz\;dy dx dz$

  2.  $\displaystyle\int_{0}^{3}\!\!\int_{0}^{1}\!\!\int_{0}^{\sqrt{1-z^{2}}}ze^{y}\;dx dz dy$

  3.  $\displaystyle\int_{0}^{\pi/2}\int_{0}^{y}\int_{0}^{x}\cos(x+y+z)\;dz dx dy$

  1.  $1.$

  2.  $\displaystyle \frac{e^3 - 1}{3}.$

  3.  $-\dfrac{1}{3}.$

2436   

Calcule a integral tripla.

  1. $\displaystyle\iiint\limits_{  E}\cos{z} \; dx dy dz$, onde $E$ é o conjunto $0\leq x \leq \dfrac{\pi}{2}$, $0\leq y \leq \dfrac{\pi}{2}$ e $x-y\leq z \leq x+y.$

  2. $\displaystyle\iiint\limits_{  E}(y-x)\;dx dy dz$, onde $E$ é o conjunto $4\leq x+y\leq 8$, $\dfrac{1}{x}\leq y\leq \dfrac{2}{x}$,  $y> x$ e $0\leq z \leq \dfrac{\sqrt[3]{xy}}{\sqrt{x+y}}.$

  1.  $2.$

  2.  $3 - 6\sqrt[3]{2} - 2\sqrt{2} + 6 \sqrt[6]{2^5}.$

2481   

Use a integral tripla para determinar o volume do sólido dado.

  1.  $0\leq x \leq 1$, $0\leq y \leq 1$ e $0\leq z \leq 5-x^{2}-3y^{2}.$

  2.  $0\leq x \leq 1$, $0\leq y \leq x^{2}$ e $0\leq z \leq x+y^{2}.$

  3. $x^{2}+y^{2}\leq z \leq 4.$

  4.  $x^{2}+4y^{2}\leq z \leq 1.$

  1.  $\dfrac{11}{3}.$

  2. $\dfrac{25}{84}.$

  3. $8\pi.$

  4.  $\dfrac{\pi}{4}.$

3052   

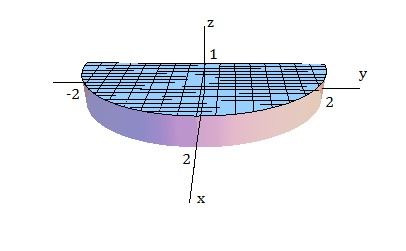
Esboce o sólido descrito pelas desigualdades $0 \leq r \leq 2$, $-\pi/2 \leq \theta \leq \pi/2$ e $0 \leq z \leq 1$.

ma211lista8q29res.png

2540   

Um cubo sólido de $2$ unidades de lado é limitado pelos planos $x=\pm 1$, $z=\pm 1$, $y=3$ e $y=5.$ Encontre o centro de massa e os momentos de inércia desse cubo.

Centro de massa: $\displaystyle \left(0,4,0 \right),$ $I_{x} = \dfrac{400}{3},$ $I_{y} = \dfrac{16}{3},$ $I_{z} = \dfrac{400}{3}.$

2537   

Suponha que o sólido tenha densidade constante $k$. Encontre os momentos de inércia para um cubo com comprimento do lado $L$ se um vértice está localizado na origem e três arestas estão nos eixos coordenados.

$\displaystyle I_{x} = I_{y} = I_{z} = \dfrac{2kL^5}{3}.$

2498   

Esboce a região limitada pelos gráficos das equações e use uma integral tripla para calcular seu volume.

  1.  $z+x^{2}=4$, $y+z=4$, $y=0$ e $z=0.$

  2.  $y=2-z^{2}$, $y=z^{2}$, $x+z=4$ e $x=0.$

  3.  $y^{2}+z^{2}=1$, $x+y+z=2$ e $x=0.$

  1.  $\dfrac{128}{5}.$

  2.  $\dfrac{32}{3}.$

  3.  $2\pi.$

3049   

 Calcule a integral tripla $\int\int\int\limits_{T}x^{2}dV$, 

onde $T$ é o tetraedro sólido com vértices $(0,0,0)$, $(1,0,0)$, $(0,1,0)$ e $(0,0,1).$


Para resolvermos a integral tripla, vamos desenhar dois diagramas: um da região sólida $T$ (Figura 1) e o outro a sua projeção $D$ no plano $xy$ (Figura 2). 

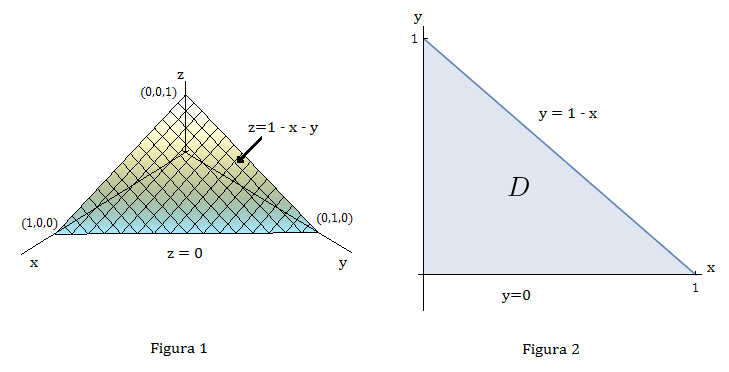
ma211lista8q1res.png

A fronteira inferior do tetraedro $T$ é o plano $z=0$ e a superior é o plano $x+y+z=1$ (ou $z=1-x-y$). 

Notemos que os planos $x+y+z=1$ e $z=0$ se interceptam na reta $x+y=1$ (ou $y=1-x$) no plano $xy.$ 

Logo a projeção de $T$ é a região triangular da Figura 2 e temos 

$$T=\{(x,y,z)|\,0\leq x \leq 1,\, 0\leq y \leq 1-x,\, 0\leq z \leq 1-x-y\}.$$

Assim, 

$$\int\int\int\limits_{T}x^{2}\,dV=\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-z}x^{2}\,dz\,dy\,dx=\int_{0}^{1}\int_{0}^{1-x}x^{2}z\bigg|_{0}^{1-x-y}\,dy\,dx$$

$$=\int_{0}^{1}\int_{0}^{1-x}x^{2}(1-x-y)\,dy\,dx=\int_{0}^{1}\int_{0}^{1-x}(x^{2}-x^{3}-x^{2}y)\,dy\,dx$$

$$=\int_{0}^{1}\bigg(x^{2}y-x^{3}y-x^{2}\frac{y^{2}}{2}\bigg)\bigg|_{0}^{1-x}\,dx=\int_{0}^{1}\bigg(x^{2}(1-x)-x^{3}(1-x)-\frac{x^{2}}{2}(1-x)^{2}\bigg)dx$$

$$=\int_{0}^{1}\bigg(\frac{x^{2}}{2}-x^{3}+\frac{x^{4}}{2}\bigg)\,dx =\bigg[\frac{1}{2}\cdot\frac{x^{3}}{3}-\frac{x^{4}}{4}+\frac{1}{2}\cdot\frac{x^{5}}{5}\bigg]\bigg|_{0}^{1}=\frac{1}{60}.$$

2533   

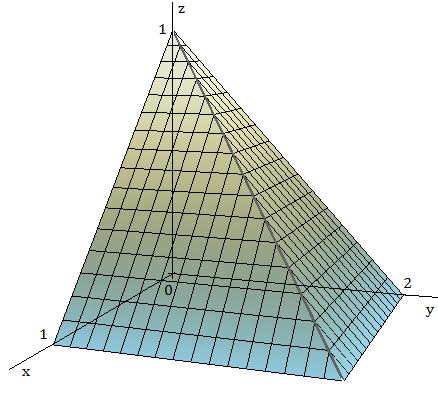
Escreva seis integrais triplas iteradas diferentes para o volume do sólido retangular no  primeiro octante limitado pelos planos coordenados e pelos planos $x=1$, $y=2$ e $z=3$. Calcule uma das integrais.

$$\begin{split} 6 &= \int_{0}^{1}\int_{0}^{2}\int_{0}^{3} dz dy dx = \int_{0}^{2}\int_{0}^{1}\int_{0}^{3} dz dx dy = \int_{0}^{3}\int_{0}^{2}\int_{0}^{1} dx dy dz\\ &= \int_{0}^{2}\int_{0}^{3}\int_{0}^{1} dx dz dy = \int_{0}^{3}\int_{0}^{1}\int_{0}^{2} dy dx dz = \int_{0}^{1}\int_{0}^{3}\int_{0}^{2} dy dx dx. \end{split} $$

3053   

Esboce o sólido cujo volume é dado pela integral iterada.

$\displaystyle\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{2-2z}\;dy dz dx$

ma211lista8q12ares.png

2428   

Calcule a integral tripla.

  1.  $\displaystyle\iiint\limits_{  E}z\,dV$, onde $E$ é limitado pelo cilindro $y^{2}+z^{2}=9$ e pelos planos $x=0$, $y=3x$ e $z=0$ no primeiro octante.

  2.  $\displaystyle\iiint\limits_{  E}xyz\;dx dy dz$, onde $E$ é o paralelepípedo $0\leq x\leq 2$, $0\leq y\leq 1$, e $1\leq z\leq 2.$

  1.  $\dfrac{27}{8}.$

  2.  $\dfrac{3}{2}.$