Superfícies parametrizadas e suas áreas

2322

Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,1-u-v)$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\dfrac{\sqrt{3}}{2}.$

2360

Encontre a área da superfície $z=1+3x+3y^{2}$ que está acima do triângulo com vértices $(0,0)$, $(0,1)$ e $(2,1).$

$\dfrac{1}{54}\left(46\sqrt{46} - 10\sqrt{10} \right).$

2323

Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,2-u-v)$ e $u^{2}+v^{2}\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\pi \sqrt{3}.$

2300

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(1,u,v)$, $0\leq u\leq 1$, $0\leq v \leq 1.$

Região quadrada do plano $x = 1:$ $0 \leq y \leq 1$ e $0 \leq z \leq 1.$

2347

Seja $f:K\rightarrow \mathbb{R}$ de classe $C^{1}$ no compacto $K$ com fronteira de conteúdo nulo e interior não-vazio. Mostre que a área da superfície $z=f(x,y)$ (isto é, da superfície ${\bf r}$ dada por $x=u$, $y=v$ e $z=f(u,v)$) é dada pela fórmula

$$\iint\limits_{ K}\sqrt{1+\bigg(\frac{\partial f}{\partial x}\bigg)^{2}+\bigg(\frac{\partial f}{\partial y}\bigg)^{2}}dxdy.$$

2359

Seja $S$ a parte do cone $x^{2}=y^{2}+z^{2}$ que está dentro do cilindro $x^{2}+y^{2}=a^{2}$ e no primeiro octante. Determine a área da superfície $S.$

$\dfrac{\pi a^2}{4}$.

2286

Identifique a superfície que tem equação paramétrica ${\bf r}(u,v)=2\,\sin u\,{\bf i}+3\,\cos u\,{\bf j}+v\,{\bf k}$, $0\leq v\leq 2.$.

$\dfrac{x^2}{4} + \dfrac{y^{2}}{9} = 1,$ com $0\leq z \leq 2.$

2292

Determine uma representação paramétrica para a superfície descrita a seguir. A parte do plano $z=x+3$ que está dentro do cilindro $x^{2}+y^{2}=1.$

$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = 3 + r \cos(\theta),$ onde $0 \leq r \leq 1$ e $0\leq \theta \leq 2\pi.$

2358

Calcule a área da parte da superfície esférica $x^{2}+y^{2}+z^{2}=1$ que se encontra dentro do cone $z\geq \sqrt{x^{2}+y^{2}}.$

$\pi(2 - \sqrt{2}).$

2305

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,1-u^{2})$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$

${\bf r}(u,v)=(u,v,1-u^{2})$, $u\geq 0$,\, $v\geq 0$ e $u+v\leq 1.$

2318

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$, no ponto ${\bf r}(1,1).$

$(x,y,z) = (1,1,2) + s(1,0,2) + t(0,1,2),$ $s,t \in \mathbb{R}.$

2289

Determine uma representação paramétrica para a superfície descrita a seguir. A parte do paraboloide elíptico $x+y^{2}+2z^{2}=4$ que está em frente ao plano $x=0.$

$y = u,$ $z = v,$ $x = 4 - u^2 - 2v^2,$ onde $u^{2} + 2v^2 \leq 4.$

3133

Encontre a massa da lâmina descrita como sendo a porção do parabolóide $2z=x^2+y^2$ que fica dentro do cilindro $x^2+y^2=8$ e tem densidade $\delta_0$ constante.

2304

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=\bigg(v\cos u,v\sin u,\dfrac{1}{v^{2}}\bigg)$, $0\leq u\leq 2\pi$, $v>0.$

Gráfico de $f(x,y) = \dfrac{1}{x^2 + y^2}.$

2324

Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$ e $u^{2}+v^{2}\leq 4.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\dfrac{\pi}{6}(17 \sqrt{17} - 1).$

2302

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,\sqrt{1-u^{2}-v^{2}},v)$, $u^{2}+v^{2}\leq 1.$

Semi superfície esférica $x^2 + y^2 + z^2 = 1,$ $y \geq 0.$

2336

Determine a área da superfície dada pela parte da superfície $z=xy$ que está dentro do cilindro $x^{2}+y^{2}=1$.

$\dfrac{2\pi}{3}(2\sqrt{2} - 1)$.

2291

Determine uma representação paramétrica para a superfície descrita a seguir. A parte do cilindro $y^{2}+z^{2}=16$ que está entre os planos $x=0$ e $x=5.$

$x = u,$ $y = 4\cos (\theta),$ $z = 4\sin(\theta),$ onde $0 \leq u \leq 5,$ $0 \leq \theta \leq 2\pi.$

2295

Determine uma representação paramétrica para a superfície descrita a seguir. A porção no primeiro octante do cone $z=\sqrt{x^{2}+y^{2}}/2$ entre os planos $z=0$ e $z=3.$

$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = \dfrac{r}{2},$ onde $0 \leq r \leq 6$ e $0\leq \theta \leq \dfrac{\pi}{2}.$

2327

Calcule a área da superfície dada por: ${\bf r}(u,v)=(\cos u,v,\sin u)$ e $u^{2}+4v^{2}\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\dfrac{\pi}{2}.$

2316

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. $x=u+v$, $y=3u^{2}$, $z=u-v$; $(2,3,0).$

$3x - y + 3z = 3.$

2337

Determine a área da superfície dada pela parte da superfície $y=4x+z^{2}$ que está entre os planos $x=0$, $x=1$, $z=0$ e $z=1.$

$\dfrac{\sqrt{21}}{2} + \dfrac{17}{4} \left( \ln(2 + \sqrt{21}) - \ln(\sqrt{17}) \right).$

2340

Determine a área da superfície dada pela parte do plano $x+2y+z=4$ que está dentro do cilindro $x^{2}+y^{2}=4$.

$4\sqrt{6}\pi.$

2299

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$, $(u,v)\in \mathbb{R}^{2}.$.

Paraboloide de rotação $z = x^2 + y^2.$

2283

Determine se os pontos $P(7,10,4)$ e $Q(5,22,5)$ estão na superfície ${\bf r}(u,v)=(2u+3v,1+5u-v,2+u+v)$.

$P$ não está na superfície; $Q$ está na superfície.

2290

Determine uma representação paramétrica para a superfície descrita a seguir. A parte da esfera $x^{2}+y^{2}+z^{2}=4$ que está acima do cone $z=\sqrt{x^{2}+y^{2}}.$

$x = 2\sin(\phi)\cos(\theta),$ $y = 2\sin(\phi)\sin(\theta),$ $z = 2\cos(\phi),$ onde $0\leq \phi \leq \frac{\pi}{4}$ e $0 \leq \theta \leq 2\pi.$

2319

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(\arctan (uv),e^{u^{2}-v^{2}},u-v)$, no ponto ${\bf r}(1,-1).$

$(x,y,z) = \left(-\dfrac{\pi}{4},1,2\right) + s\left(-\dfrac{1}{2},2,1\right) + t\left(\dfrac{1}{2},2,-1\right),$ $s,t \in \mathbb{R}.$

2294

Determine uma representação paramétrica para a superfície descrita a seguir. O paraboloide $z=9-x^{2}-y^{2}$, $z\geq 0.$

$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = 9 - r^2,$ onde $0 \leq r \leq 3$ e $0\leq \theta \leq 2\pi.$

2345

Mostre que as equações paramétricas $x=a \cosh u\cos v$, $y=b\cosh u \sin v$, $z=c\sinh u$, representam um hiperboloide de uma folha.

Note que $\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} - \dfrac{z^{2}}{c^{2}} = 1$.

2301

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,1-u-v)$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$

Região triangular do plano $x + y + z = 1:$ $0 \leq x \leq 1, $ $0 \leq y \leq 1,$ $0 \leq z \leq 1.$

3132

Encontre a massa da lâmina descrita como sendo a porção do cilindro circular $x^2+z^2=4$ que fica diretamente acima do retângulo $\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq x\leq 1,\ 0\leq y\leq 4\}$ e tem densidade $\delta_0$ constante.

$\dfrac{4}{3}\pi\delta_0$

2346

Encontre a área da parte da esfera $x^{2}+y^{2}+z^{2}=a^{2}$ que está dentro do cilindro $x^{2}+y^{2}=ax.$

$2a^2 (\pi - 2).$

2326

Calcule a área da superfície dada por: ${\bf r}(u,v)=\bigg(u,v,\dfrac{1}{2}u^{2}\bigg)$,$0\leq v\leq u$ e $u\leq 2.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\dfrac{1}{3}\left(5\sqrt{5} - 1 \right).$

2303

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(v\,\cos u,v\sin u,v)$, $0\leq u\leq 2\pi$,\, $0\leq v \leq h$, onde $h>0$ é um real dado.

Face lateral do cone $\sqrt{x^{2} + y^{2}} \leq z \leq h$.

2343

Seja $A=\{(0,y,z)\in \mathbb{R}^{3}| z^{2}+(y-2)^{2}=1\}$; ache a área da superfície gerada pela rotação em torno do eixo $Oz$ do conjunto $A.$

$8\pi^2.$

2328

Determine a área da superfície dada pela parte do plano $3x+2y+z=6$ que está no primeiro octante.

$3\sqrt{14}.$

2284

Determine se os pontos $P(3,-1,5)$ e $Q(-1,3,4)$ estão na superfície ${\bf r}(u,v)=(u+v,u^{2}-v,u+v^{2})$.

$P$ está na superfície; $Q$ não está na superfície.

2287

Determine uma representação paramétrica para a superfície descrita a seguir. O plano que passa pelo ponto $(1,2,-3)$ e contém os vetores ${\bf i}+{\bf j}-{\bf k}$ e ${\bf i}-{\bf j}+{\bf k}.$

$x= 1 + u + v,$ $y = 2 + u - v,$ $z = 3 - u + v.$

2344

Determine, mas não calcule, a integral dupla da área da superfície com as equações paramétricas $x=au\cos v$, $y=bu\sin v$, $z=u^{2}$, $0\leq u\leq 2$, $0\leq v\leq 2\pi.$
Elimine os parâmetros para mostrar que a superfície é um paraboloide elíptico e escreva outra integral dupla que forneça sua área.

$\displaystyle \int^{2\pi}_{0}\int_{0}^{2} \sqrt{4b^2 u^4 \cos^{2}v + 4a^2 u^4 \sin^{2} v + a^2 b^2 u^2} dudv.$
$\displaystyle \int_{-2a}^{2a} \int^{b \sqrt{4 - \frac{x^2}{a^2}}}_{-b \sqrt{4 - \frac{x^2}{a^2}}} \sqrt{1 + \left(2\frac{x}{a^2}\right)^{2} + \left(2\frac{y}{b^2} \right)^{2}} dydx.$

2320

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(3\sin 2u,6\sin^{2} u, v)$,$0\leq u\leq \pi$, no ponto ${\bf r}(\pi/3,0).$

$x^{2} + (y-3)^{2} = 9.$

2270

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(u-v,u^{2}+v^{2},uv)$, no ponto ${\bf r}(1,1).$

Temos que ${\bf r}(u,v)=\underbrace{(u-v)}_{x(u,v)}\,{\bf i}+\underbrace{(u^{2}+v^{2})}_{y(u,v)}\,{\bf j}+\underbrace{uv}_{z(u,v)}\,{\bf k}$

Primeiro, vamos calcular os vetores tangentes:

$$\begin{array}{rcl}{\bf r}_{u}&=&\frac{\partial x(u,v)}{\partial u}\,{\bf i}+\frac{\partial y(u,v)}{\partial u}\,{\bf j}+\frac{\partial z(u,v)}{\partial u}\,{\bf k}\\&=& \,{\bf i}+2u\,{\bf j}+v\,{\bf k}\end{array}$$

e

$$\begin{array}{rcl}{\bf r}_{v}&=&\frac{\partial x(u,v)}{\partial v}\,{\bf i}+\frac{\partial y(u,v)}{\partial v}\,{\bf j}+\frac{\partial z(u,v)}{\partial v}\,{\bf k}\\&=& -\,{\bf i}+2v\,{\bf j}+u\,{\bf k}\end{array}$$

Assim, o vetor normal ao plano tangente é:

$$\begin{array}{rcl}{\bf r}_{u}\times {\bf r}_{v}&=&\left|\begin{array}{ccc}{\bf i}& {\bf j}&{\bf k}\\1 & 2u & v\\-1 & 2v & u\\\end{array}\right|\\&=&(-2u^{2}-2v^{2})\,{\bf i}-(u+v)\,{\bf j}+(2u+2v)\,{\bf k}\end{array}$$

Como $u=1$ e $v=1$ temos que o vetor normal é $-4\,{\bf i}-2\,{\bf j}+4\,{\bf k}.$

Portanto, uma equação do plano tangente no ponto ${\bf r}(1,1)=(0,2,1)$ é

$$-4\cdot(x-0)-2\cdot(y-2)+4\cdot (z-1)=0$$

$$-4x-2y+4+4z-4=0$$

$$-4x-2y+4z=0 \mbox{ou} 2x+y-2z=0$$

2269

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=u^{2}\,{\bf i}+2u\,\sin v\,{\bf j}+u\,\cos v\,{\bf k}$; $u=1$, $v=0.$

Temos que ${\bf r}(u,v)=\underbrace{u^{2}}_{x(u,v)}\,{\bf i}+\underbrace{2u\,\sin v}_{y(u,v)}\,{\bf j}+\underbrace{u\,\cos v}_{z(u,v)}\,{\bf k}$

Primeiro, vamos calcular os vetores tangentes:

$$\begin{array}{rcl}{\bf r}_{u}&=&\frac{\partial x(u,v)}{\partial u}\,{\bf i}+\frac{\partial y(u,v)}{\partial u}\,{\bf j}+\frac{\partial z(u,v)}{\partial u}\,{\bf k}\\&=& 2u\,{\bf i}+2\,\sin v\,{\bf j}+\cos v\,{\bf k}\end{array}$$

e

$$\begin{array}{rcl}{\bf r}_{v}&=&\frac{\partial x(u,v)}{\partial v}\,{\bf i}+\frac{\partial y(u,v)}{\partial v}\,{\bf j}+\frac{\partial z(u,v)}{\partial v}\,{\bf k}\\&=& 0\,{\bf i}+2u\,\cos v\,{\bf j}-u\sin v\,{\bf k}\end{array}$$

Assim, o vetor normal ao plano tangente é:

$$\begin{array}{rcl}{\bf r}_{u}\times {\bf r}_{v}&=&\left|\begin{array}{ccc}{\bf i} & {\bf j} & {\bf k}\\2u & 2\sin v & \cos v\\0 & 2u\cos v & -u\sin v\\\end{array}\right|\\&=&(-2u\,\sin^{2}v-2u\cos^{2}v)\,{\bf i}+(2u^{2}\,\sin v)\,{\bf j}+(4u^{2}\,\cos v)\,{\bf k}\end{array}$$

Como $u=1$ e $v=0$ temos que o vetor normal é $-2\,{\bf i}+0\,{\bf j}+4\,{\bf k}.$

Portanto, uma equação do plano tangente no ponto ${\bf r}(1,0)=(1,0,1)$ é

$$-2\cdot(x-1)+0\cdot(y-0)+4\cdot (z-1)=0$$

$$-2x+2+4z-4=0$$

$$-2x+4z-2=0 \mbox{ou} x-2z+1=0$$

2341

Determine a área da superfície dada pela porção do cone $z=2\sqrt{x^{2}+y^{2}}$ entre os planos $z=2$ e $z=6.$

$8\sqrt{5}\pi.$

2338

Determine a área da superfície $z=\frac{2}{3}(x^{3/2}+y^{3/2})$, $0\leq x \leq 1$ e $0\leq y\leq 1.$

$\dfrac{4}{15}(3^{5/2} - 2^{7/2} + 1).$

2342

Determine a área da superfície dada pela porção do cilindro $x^{2}+y^{2}=1$ entre os planos $z=1$ e $z=4.$

$6\pi.$

2361

Considere a superfície parametrizada por

$${\bf r}(u,v)=(uv,u+v,u-v).$$

Determine o valor de $c$ de forma que o ponto $(c,1,0)$ pertença à superfície.
Calcule a área da parte da superfície correspondente à variação $u^{2}+v^{2}\leq 1.$

$\dfrac{1}{4}.$
$\left(\sqrt{6} - \dfrac{4}{3} \right)2\pi.$

2317

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. $x=u^{2}$, $y=v^{2}$, $z=uv$; $u=1$, $v=1.$

$x + y - 2z = 0.$

3042

Determine a representação paramétrica do toro obtido girando em torno do eixo $z$ o círculo do plano $xz$ com centro em $(b,0,0)$ e raio $a < b.$ [Sugestão: tome como parâmetros os ângulos $\theta$ e $\alpha$ mostrados na figura.]
Use a representação paramétrica do item anterior para achar a área do toro.

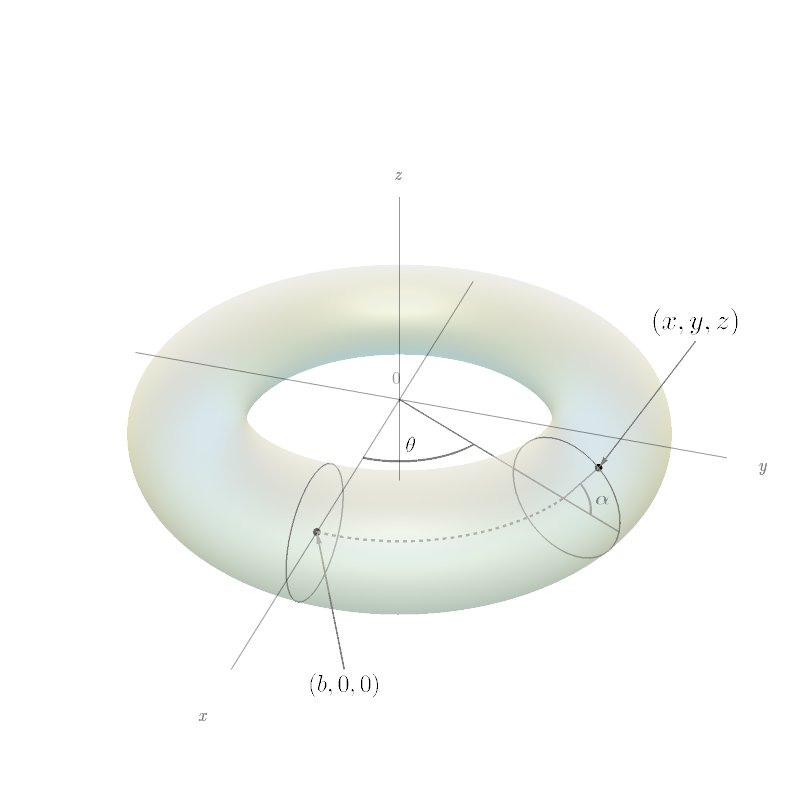
$x = b\cos(\theta) + a\cos(\alpha)\cos(\theta),$ $y = b\sin(\theta) + a\cos(\alpha)\sin(\theta),$ $z = a\sin(\alpha),$ onde $0 \leq \alpha \leq 2\pi,$ $0 \leq \theta \leq 2\pi.$
$4\pi^2 ab.$

2288

Determine uma representação paramétrica para a superfície descrita a seguir. A parte do hiperboloide $x^{2}+y^{2}-z^{2}=1$ que está à direita do plano $xz.$

$x =u,$ $z = v,$ $y = \sqrt{1 - u^2 + v^2}.$

2298

Determine uma representação paramétrica para a superfície descrita a seguir. A porção do cilindro $(x-2)^{2}+z^{2}=4$ entre os planos $y=0$ e $y=3.$

$x = 4\cos^{2}(v),$ $y = u,$ $z = 4\cos(v)\sin(v),$ onde $-\dfrac{\pi}{2}\leq v \leq \dfrac{\pi}{2}$ e $0 \leq u \leq 3.$

3041

Faça uma correspondência entre as equações e os gráficos identificados a seguir, enumerador respectivamente por $I-VI$, e justifique sua resposta. Determine quais famílias de curvas da grade têm $u$ constante e quais têm $v$ constante.

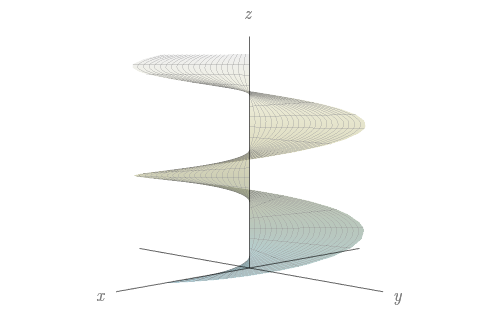
${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+v{\bf k}.$
${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+\sin u{\bf k}$, $-\pi\leq u\leq \pi.$
${\bf r}(u,v)=\sin v{\bf i}+\cos u\sin 2v{\bf j}+\sin u\sin 2v{\bf k}.$
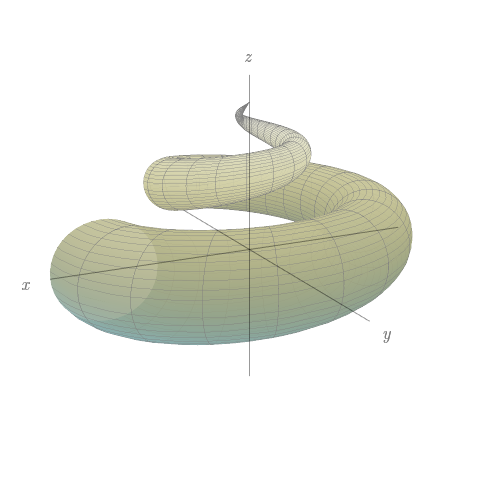
$x=(1-u)(3+\cos v)\cos 4\pi u$, $y=(1-u)(3+\cos v)\sin 4\pi u$,$z=3u+(1-u)\sin v.$
$x=\cos^{3}u\cos^{3}v$, $y=\sin^{3}u\cos^{3}v$, $z=\sin^{3}v.$
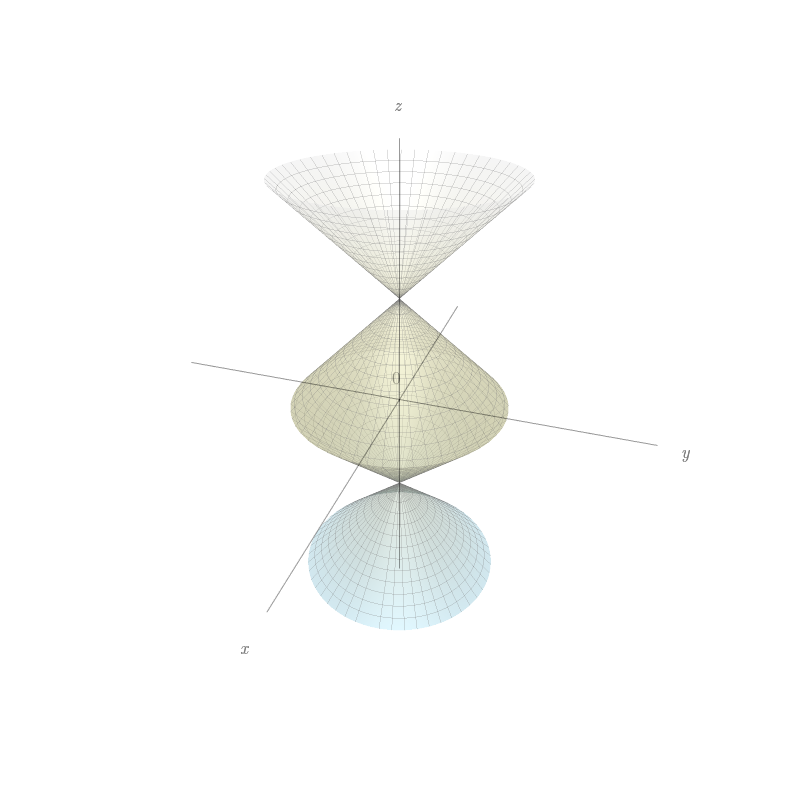
$x=(1-|u|)\cos v$, $y=(1-|u|)\sin v$, $z=u.$

IV.
I.
II.
V.
III.
VI

2325

Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,4-u^{2}-v^{2})$, $(u,v)\in K$, onde $K$ é o conjunto no plano $uv$ limitado pelo eixo $u$ e pela curva (em coordenadas polares) $\rho=e^{-\theta}$,$0\leq \theta \leq \pi.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\displaystyle \dfrac{1}{72} \left( \ln\left(3\dfrac{\sqrt{e^{2\pi} + 4} + e^{\pi}}{\sqrt{e^{2\pi} + 4} - e^{\pi}} \right) + 3 \ln\left(\dfrac{\sqrt{5} - 1 }{\sqrt{5} + 1 }\right) - 8e^{3\pi} \sqrt{e^{2\pi} + 4}(e^{2\pi} + 1) + 16\sqrt{5} - 6\pi \right).$

2348

Calcule a área da parte da superfície cilíndrica $z^{2}+x^{2}=4$ que se encontra dentro do cilindro $x^{2}+y^{2}\leq 4$ e acima do plano $xy.$

$16.$

2339

Determine a área da superfície com equações paramétricas $x=u^{2}$, $y=uv$, $z=\dfrac{1}{2}v^{2}$, $0\leq u\leq 1$, $0\leq v\leq 2.$

$4.$

2268

Determine a área da superfície dada pela parte de baixo da esfera $x^{2}+y^{2}+z^{2}=2$ cortada pelo cone $z=\sqrt{x^{2}+y^{2}}.$

Sejam

$$\left \{\begin{array}{cc}x=r\,\sin \phi\,\cos \theta\\y=r\,\sin \phi\,\sin \theta\\z=r\,\cos \phi\\\end{array}\right. \Rightarrow r=\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{2},\, \mbox{na\,esfera}.$$

Temos que

$$x^{2}+y^{2}+z^{2}=2 \mbox{e}\,\,\,\, z=\sqrt{x^{2}+y^{2}}\Rightarrow z^{2}+z^{2}=2\Rightarrow z^{2}=1\Rightarrow z=1\,(\mbox{pois}\, z\geq 0).$$

Logo, $\phi=\frac{\pi}{4}.$ Para a parte inferior da esfera cortado pelo cone, temos que $\phi=\pi.$

Então,

$$r(\phi,\theta)=(\sqrt{2}\,\sin \phi,\,\cos\theta)\,{\bf i}+(\sqrt{2}\,\sin \phi\,\sin \theta)\,{\bf j}+(\sqrt{2}\,\cos \phi)\,{\bf k},$$

$$\frac{\pi}{4}\leq \phi\leq \pi\,\,\,\, \mbox{e}\,\,\,\, 0\leq \theta \leq 2\pi.$$

Isso implica que

$$r_{\phi}(\phi,\theta)=(\sqrt{2}\,\cos \phi,\,\cos\theta)\,{\bf i}+(\sqrt{2}\,\cos \phi\,\sin \theta)\,{\bf j}-(\sqrt{2}\,\sin \phi)\,{\bf k}$$

e

$$r_{\theta}(\phi,\theta)=(-\sqrt{2}\,\sin \phi,\,\sin\theta)\,{\bf i}+(\sqrt{2}\,\sin \phi\,\cos \theta)\,{\bf j}+0\,{\bf k}$$

Logo,

$$\begin{array}{rcl}r_{\phi}\times r_{\theta}&=&\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\\sqrt{2}\,\cos \phi\,\cos \theta & \sqrt{2}\,\cos \phi\,\sin \theta& -\sqrt{2}\,\sin \phi\\-\sqrt{2}\,\sin \phi\,\sin \theta & \sqrt{2}\,\sin \phi\,\cos \theta & 0\end{array}\right|\\&=&(2\,\sin^{2}\phi\,\cos \theta)\,{\bf i}+(2\sin^{2}\phi\,\sin \theta)\,{\bf j}+(2\,\sin \phi \,\cos \phi)\,{\bf k}.\\\end{array}$$

Isso resulta que

$$\begin{array}{rcl}|r_{\phi}\times r_{\theta}|&=&\sqrt{4\sin^{2}\phi\,\cos^{2}\theta+4\,\sin^{4}\,\sin^{2}\theta+4\sin^{2}\phi\,\cos^{2}\phi}\\&=&\sqrt{4\,\sin^{2}\phi}=2|\sin\phi|=2\sin \phi \bigg(\mbox{pois},\, \frac{\pi}{4}\leq \phi \leq \pi\bigg).\end{array}$$

Assim,

$$A=\iint\limits_{ D}|r_{\phi}\times r_{\theta}|\,dA=\int_{\frac{\pi}{4}}^{\pi}\int_{0}^{2\pi}2\sin \phi\, d\theta d \phi=2\int_{\frac{\pi}{4}}^{\pi}\sin \phi\,d\phi \cdot \int_{0}^{2\pi}d\theta$$

$$=2\cdot (-\cos \phi)\bigg|_{\frac{\pi}{4}}^{\pi}\cdot \theta\bigg|_{0}^{2\pi}=2\cdot \bigg(1-\frac{\sqrt{2}}{2}\bigg)\cdot 2\pi=4\pi\bigg(1-\frac{\sqrt{2}}{2}\bigg)=\pi(4-2\sqrt{2})$$

2297

Determine uma representação paramétrica para a superfície descrita a seguir. A superfície cortada do cilindro parabólico $z=4-y^{2}$ pelos planos $x=0$, $x=2$ e $z=0.$

$x = u,$ $y = v,$ $z = 4 - v^2,$ onde $0\leq u \leq 2$ e $-2 \leq v \leq 2.$

2296

Determine uma representação paramétrica para a superfície descrita a seguir. A porção da esfera $x^{2}+y^{2}+z^{2}=3$ entre os planos $z=\sqrt{3}/2$ e $z=-\sqrt{3}/2.$

$x = \sqrt{3}\sin(\phi)\cos(\theta),$ $y = \sqrt{3}\sin(\phi)\sin(\theta),$ $z = \sqrt{3}\cos(\phi),$ onde $\dfrac{\pi}{3} \leq \phi \leq \dfrac{2\pi}{3}$ e $0 \leq \theta \leq 2\pi.$

2267

Determine a área da superfície dada pela parte do paraboloide hiperbólico $z=y^{2}-x^{2}$ que está entre os cilindros $x^{2}+y^{2}=1$ e $x^{2}+y^{2}=4.$

Temos que $z=f(x,y)=y^{2}-x^{2}$ com $1\leq x^{2}+y^{2}\leq 4$. Então,

$$A(S)=\iint\limits_{ D}\sqrt{1+\bigg(\frac{\partial z}{\partial x}\bigg)^{2}+\bigg(\frac{\partial z}{\partial y}\bigg)^{2}}\,dA$$

$$=\iint\limits_{ D}\sqrt{1+(2y)^{2}+(-2x)^{2}}\,dA=\iint\limits_{ D}\sqrt{1+4y^{2}+4x^{2}}\,dA.$$

Usando coordenadas polares temos que

$$x=r\,\cos \theta,\,\,\,\,\, y=r\,\sin \theta \Rightarrow 0\leq \theta\leq \frac{\pi}{2}\,\, \mbox{e}\,\, 1\leq r \leq 2.$$

Assim,

$$A(S)=\int_{0}^{2\pi}\int_{1}^{2}\sqrt{1+4r^{2}}\,r\,dr\,d\theta=\int_{0}^{2\pi}d\theta \cdot \underbrace{\int_{1}^{2}\sqrt{1+4r^{2}}r\,dr}_{\substack{u=1+4r^{2}\\ du=8r\,dr}}$$

$$=\theta\bigg|_{0}^{2\pi}\cdot \int_{5}^{17}u^{1/2}\cdot r\cdot \frac{du}{8r}=2\pi\cdot \frac{1}{8}\int_{5}^{17}u^{1/2}\,du=\frac{\pi}{4}\cdot \frac{2}{3}u^{3/2}\bigg|_{5}^{17}$$

$$=\frac{\pi}{6}\cdot(17^{3/2}-5^{3/2}).$$

2293

Determine uma representação paramétrica para a superfície descrita a seguir. O paraboloide $z=x^{2}+y^{2}$, \, $z\leq 4.$

$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = r^2,$ onde $0 \leq r \leq 2$ e $0\leq \theta \leq 2\pi.$

2285

Identifique a superfície que tem equação paramétrica ${\bf r}(u,v)=(u+v)\,{\bf i}+(3-v)\,{\bf j}+(1+4u+5v)\,{\bf k}.$.

$4x - y - z = -4.$

2321

Determine uma representação paramétrica ${\bf r}:D\subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}$ do paraboloide elíptico $z=\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}.$
Calcule a equação do plano tangente à superfície paramétrica dada no item (a) no ponto $(-a\pi,0,\pi^{2}).$

$x = u,$ $y = v,$ $z = \dfrac{u^{2}}{a^{2}}+\dfrac{v^{2}}{b^{2}},$ onde $u,v \in \mathbb{R}.$
$2\pi(x + a\pi) + a(z - \pi^{2}) = 0.$