Superfícies parametrizadas e suas áreas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Determine a área da superfície dada pela parte da superfície $z=xy$ que está dentro do cilindro $x^{2}+y^{2}=1$.
$\dfrac{2\pi}{3}(2\sqrt{2} - 1)$.
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=\bigg(v\cos u,v\sin u,\dfrac{1}{v^{2}}\bigg)$, $0\leq u\leq 2\pi$, $v>0.$
Gráfico de $f(x,y) = \dfrac{1}{x^2 + y^2}.$
Considere a superfície parametrizada por
$${\bf r}(u,v)=(uv,u+v,u-v).$$
Determine o valor de $c$ de forma que o ponto $(c,1,0)$ pertença à superfície.
Calcule a área da parte da superfície correspondente à variação $u^{2}+v^{2}\leq 1.$
$\dfrac{1}{4}.$
$\left(\sqrt{6} - \dfrac{4}{3} \right)2\pi.$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(3\sin 2u,6\sin^{2} u, v)$,$0\leq u\leq \pi$, no ponto ${\bf r}(\pi/3,0).$
$x^{2} + (y-3)^{2} = 9.$
Mostre que as equações paramétricas $x=a \cosh u\cos v$, $y=b\cosh u \sin v$, $z=c\sinh u$, representam um hiperboloide de uma folha.
Note que $\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} - \dfrac{z^{2}}{c^{2}} = 1$.
Seja $A=\{(0,y,z)\in \mathbb{R}^{3}| z^{2}+(y-2)^{2}=1\}$; ache a área da superfície gerada pela rotação em torno do eixo $Oz$ do conjunto $A.$
$8\pi^2.$
Calcule a área da parte da superfície esférica $x^{2}+y^{2}+z^{2}=1$ que se encontra dentro do cone $z\geq \sqrt{x^{2}+y^{2}}.$
$\pi(2 - \sqrt{2}).$
Determine a área da superfície dada pela porção do cilindro $x^{2}+y^{2}=1$ entre os planos $z=1$ e $z=4.$
$6\pi.$
Determine uma representação paramétrica ${\bf r}:D\subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}$ do paraboloide elíptico $z=\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}.$
Calcule a equação do plano tangente à superfície paramétrica dada no item (a) no ponto $(-a\pi,0,\pi^{2}).$
$x = u,$ $y = v,$ $z = \dfrac{u^{2}}{a^{2}}+\dfrac{v^{2}}{b^{2}},$ onde $u,v \in \mathbb{R}.$
$2\pi(x + a\pi) + a(z - \pi^{2}) = 0.$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$, no ponto ${\bf r}(1,1).$
$(x,y,z) = (1,1,2) + s(1,0,2) + t(0,1,2),$ $s,t \in \mathbb{R}.$
Determine a representação paramétrica do toro obtido girando em torno do eixo $z$ o círculo do plano $xz$ com centro em $(b,0,0)$ e raio $a < b.$ [Sugestão: tome como parâmetros os ângulos $\theta$ e $\alpha$ mostrados na figura.]
Use a representação paramétrica do item anterior para achar a área do toro.

$x = b\cos(\theta) + a\cos(\alpha)\cos(\theta),$ $y = b\sin(\theta) + a\cos(\alpha)\sin(\theta),$ $z = a\sin(\alpha),$ onde $0 \leq \alpha \leq 2\pi,$ $0 \leq \theta \leq 2\pi.$
$4\pi^2 ab.$
Identifique a superfície que tem equação paramétrica ${\bf r}(u,v)=(u+v)\,{\bf i}+(3-v)\,{\bf j}+(1+4u+5v)\,{\bf k}.$.
$4x - y - z = -4.$
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,1-u-v)$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$
Região triangular do plano $x + y + z = 1:$ $0 \leq x \leq 1, $ $0 \leq y \leq 1,$ $0 \leq z \leq 1.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(\cos u,v,\sin u)$ e $u^{2}+4v^{2}\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\dfrac{\pi}{2}.$
Determine, mas não calcule, a integral dupla da área da superfície com as equações paramétricas $x=au\cos v$, $y=bu\sin v$, $z=u^{2}$, $0\leq u\leq 2$, $0\leq v\leq 2\pi.$
Elimine os parâmetros para mostrar que a superfície é um paraboloide elíptico e escreva outra integral dupla que forneça sua área.
$\displaystyle \int^{2\pi}_{0}\int_{0}^{2} \sqrt{4b^2 u^4 \cos^{2}v + 4a^2 u^4 \sin^{2} v + a^2 b^2 u^2} dudv.$
$\displaystyle \int_{-2a}^{2a} \int^{b \sqrt{4 - \frac{x^2}{a^2}}}_{-b \sqrt{4 - \frac{x^2}{a^2}}} \sqrt{1 + \left(2\frac{x}{a^2}\right)^{2} + \left(2\frac{y}{b^2} \right)^{2}} dydx.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=\bigg(u,v,\dfrac{1}{2}u^{2}\bigg)$,$0\leq v\leq u$ e $u\leq 2.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\dfrac{1}{3}\left(5\sqrt{5} - 1 \right).$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte do cilindro $y^{2}+z^{2}=16$ que está entre os planos $x=0$ e $x=5.$
$x = u,$ $y = 4\cos (\theta),$ $z = 4\sin(\theta),$ onde $0 \leq u \leq 5,$ $0 \leq \theta \leq 2\pi.$
Determine a área da superfície com equações paramétricas $x=u^{2}$, $y=uv$, $z=\dfrac{1}{2}v^{2}$, $0\leq u\leq 1$, $0\leq v\leq 2.$
$4.$
Determine a área da superfície dada pela parte do plano $3x+2y+z=6$ que está no primeiro octante.
$3\sqrt{14}.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,2-u-v)$ e $u^{2}+v^{2}\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\pi \sqrt{3}.$
Determine uma representação paramétrica para a superfície descrita a seguir. A porção da esfera $x^{2}+y^{2}+z^{2}=3$ entre os planos $z=\sqrt{3}/2$ e $z=-\sqrt{3}/2.$
$x = \sqrt{3}\sin(\phi)\cos(\theta),$ $y = \sqrt{3}\sin(\phi)\sin(\theta),$ $z = \sqrt{3}\cos(\phi),$ onde $\dfrac{\pi}{3} \leq \phi \leq \dfrac{2\pi}{3}$ e $0 \leq \theta \leq 2\pi.$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte do paraboloide elíptico $x+y^{2}+2z^{2}=4$ que está em frente ao plano $x=0.$
$y = u,$ $z = v,$ $x = 4 - u^2 - 2v^2,$ onde $u^{2} + 2v^2 \leq 4.$
Determine a área da superfície dada pela parte do paraboloide hiperbólico $z=y^{2}-x^{2}$ que está entre os cilindros $x^{2}+y^{2}=1$ e $x^{2}+y^{2}=4.$
Temos que $z=f(x,y)=y^{2}-x^{2}$ com $1\leq x^{2}+y^{2}\leq 4$. Então,
$$A(S)=\iint\limits_{ D}\sqrt{1+\bigg(\frac{\partial z}{\partial x}\bigg)^{2}+\bigg(\frac{\partial z}{\partial y}\bigg)^{2}}\,dA$$
$$=\iint\limits_{ D}\sqrt{1+(2y)^{2}+(-2x)^{2}}\,dA=\iint\limits_{ D}\sqrt{1+4y^{2}+4x^{2}}\,dA.$$
Usando coordenadas polares temos que
$$x=r\,\cos \theta,\,\,\,\,\, y=r\,\sin \theta \Rightarrow 0\leq \theta\leq \frac{\pi}{2}\,\, \mbox{e}\,\, 1\leq r \leq 2.$$
Assim,
$$A(S)=\int_{0}^{2\pi}\int_{1}^{2}\sqrt{1+4r^{2}}\,r\,dr\,d\theta=\int_{0}^{2\pi}d\theta \cdot \underbrace{\int_{1}^{2}\sqrt{1+4r^{2}}r\,dr}_{\substack{u=1+4r^{2}\\ du=8r\,dr}}$$
$$=\theta\bigg|_{0}^{2\pi}\cdot \int_{5}^{17}u^{1/2}\cdot r\cdot \frac{du}{8r}=2\pi\cdot \frac{1}{8}\int_{5}^{17}u^{1/2}\,du=\frac{\pi}{4}\cdot \frac{2}{3}u^{3/2}\bigg|_{5}^{17}$$
$$=\frac{\pi}{6}\cdot(17^{3/2}-5^{3/2}).$$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=u^{2}\,{\bf i}+2u\,\sin v\,{\bf j}+u\,\cos v\,{\bf k}$; $u=1$, $v=0.$
Temos que ${\bf r}(u,v)=\underbrace{u^{2}}_{x(u,v)}\,{\bf i}+\underbrace{2u\,\sin v}_{y(u,v)}\,{\bf j}+\underbrace{u\,\cos v}_{z(u,v)}\,{\bf k}$
Primeiro, vamos calcular os vetores tangentes:
$$\begin{array}{rcl}{\bf r}_{u}&=&\frac{\partial x(u,v)}{\partial u}\,{\bf i}+\frac{\partial y(u,v)}{\partial u}\,{\bf j}+\frac{\partial z(u,v)}{\partial u}\,{\bf k}\\&=& 2u\,{\bf i}+2\,\sin v\,{\bf j}+\cos v\,{\bf k}\end{array}$$
e
$$\begin{array}{rcl}{\bf r}_{v}&=&\frac{\partial x(u,v)}{\partial v}\,{\bf i}+\frac{\partial y(u,v)}{\partial v}\,{\bf j}+\frac{\partial z(u,v)}{\partial v}\,{\bf k}\\&=& 0\,{\bf i}+2u\,\cos v\,{\bf j}-u\sin v\,{\bf k}\end{array}$$
Assim, o vetor normal ao plano tangente é:
$$\begin{array}{rcl}{\bf r}_{u}\times {\bf r}_{v}&=&\left|\begin{array}{ccc}{\bf i} & {\bf j} & {\bf k}\\2u & 2\sin v & \cos v\\0 & 2u\cos v & -u\sin v\\\end{array}\right|\\&=&(-2u\,\sin^{2}v-2u\cos^{2}v)\,{\bf i}+(2u^{2}\,\sin v)\,{\bf j}+(4u^{2}\,\cos v)\,{\bf k}\end{array}$$
Como $u=1$ e $v=0$ temos que o vetor normal é $-2\,{\bf i}+0\,{\bf j}+4\,{\bf k}.$
Portanto, uma equação do plano tangente no ponto ${\bf r}(1,0)=(1,0,1)$ é
$$-2\cdot(x-1)+0\cdot(y-0)+4\cdot (z-1)=0$$
$$-2x+2+4z-4=0$$
$$-2x+4z-2=0 \mbox{ou} x-2z+1=0$$
Determine a área da superfície dada pela parte de baixo da esfera $x^{2}+y^{2}+z^{2}=2$ cortada pelo cone $z=\sqrt{x^{2}+y^{2}}.$
Sejam
$$\left \{\begin{array}{cc}x=r\,\sin \phi\,\cos \theta\\y=r\,\sin \phi\,\sin \theta\\z=r\,\cos \phi\\\end{array}\right. \Rightarrow r=\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{2},\, \mbox{na\,esfera}.$$
Temos que
$$x^{2}+y^{2}+z^{2}=2 \mbox{e}\,\,\,\, z=\sqrt{x^{2}+y^{2}}\Rightarrow z^{2}+z^{2}=2\Rightarrow z^{2}=1\Rightarrow z=1\,(\mbox{pois}\, z\geq 0).$$
Logo, $\phi=\frac{\pi}{4}.$ Para a parte inferior da esfera cortado pelo cone, temos que $\phi=\pi.$
Então,
$$r(\phi,\theta)=(\sqrt{2}\,\sin \phi,\,\cos\theta)\,{\bf i}+(\sqrt{2}\,\sin \phi\,\sin \theta)\,{\bf j}+(\sqrt{2}\,\cos \phi)\,{\bf k},$$
$$\frac{\pi}{4}\leq \phi\leq \pi\,\,\,\, \mbox{e}\,\,\,\, 0\leq \theta \leq 2\pi.$$
Isso implica que
$$r_{\phi}(\phi,\theta)=(\sqrt{2}\,\cos \phi,\,\cos\theta)\,{\bf i}+(\sqrt{2}\,\cos \phi\,\sin \theta)\,{\bf j}-(\sqrt{2}\,\sin \phi)\,{\bf k}$$
e
$$r_{\theta}(\phi,\theta)=(-\sqrt{2}\,\sin \phi,\,\sin\theta)\,{\bf i}+(\sqrt{2}\,\sin \phi\,\cos \theta)\,{\bf j}+0\,{\bf k}$$
Logo,
$$\begin{array}{rcl}r_{\phi}\times r_{\theta}&=&\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\\sqrt{2}\,\cos \phi\,\cos \theta & \sqrt{2}\,\cos \phi\,\sin \theta& -\sqrt{2}\,\sin \phi\\-\sqrt{2}\,\sin \phi\,\sin \theta & \sqrt{2}\,\sin \phi\,\cos \theta & 0\end{array}\right|\\&=&(2\,\sin^{2}\phi\,\cos \theta)\,{\bf i}+(2\sin^{2}\phi\,\sin \theta)\,{\bf j}+(2\,\sin \phi \,\cos \phi)\,{\bf k}.\\\end{array}$$
Isso resulta que
$$\begin{array}{rcl}|r_{\phi}\times r_{\theta}|&=&\sqrt{4\sin^{2}\phi\,\cos^{2}\theta+4\,\sin^{4}\,\sin^{2}\theta+4\sin^{2}\phi\,\cos^{2}\phi}\\&=&\sqrt{4\,\sin^{2}\phi}=2|\sin\phi|=2\sin \phi \bigg(\mbox{pois},\, \frac{\pi}{4}\leq \phi \leq \pi\bigg).\end{array}$$
Assim,
$$A=\iint\limits_{ D}|r_{\phi}\times r_{\theta}|\,dA=\int_{\frac{\pi}{4}}^{\pi}\int_{0}^{2\pi}2\sin \phi\, d\theta d \phi=2\int_{\frac{\pi}{4}}^{\pi}\sin \phi\,d\phi \cdot \int_{0}^{2\pi}d\theta$$
$$=2\cdot (-\cos \phi)\bigg|_{\frac{\pi}{4}}^{\pi}\cdot \theta\bigg|_{0}^{2\pi}=2\cdot \bigg(1-\frac{\sqrt{2}}{2}\bigg)\cdot 2\pi=4\pi\bigg(1-\frac{\sqrt{2}}{2}\bigg)=\pi(4-2\sqrt{2})$$
Determine uma representação paramétrica para a superfície descrita a seguir. O plano que passa pelo ponto $(1,2,-3)$ e contém os vetores ${\bf i}+{\bf j}-{\bf k}$ e ${\bf i}-{\bf j}+{\bf k}.$
$x= 1 + u + v,$ $y = 2 + u - v,$ $z = 3 - u + v.$
Determine a área da superfície dada pela porção do cone $z=2\sqrt{x^{2}+y^{2}}$ entre os planos $z=2$ e $z=6.$
$8\sqrt{5}\pi.$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte do plano $z=x+3$ que está dentro do cilindro $x^{2}+y^{2}=1.$
$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = 3 + r \cos(\theta),$ onde $0 \leq r \leq 1$ e $0\leq \theta \leq 2\pi.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$ e $u^{2}+v^{2}\leq 4.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\dfrac{\pi}{6}(17 \sqrt{17} - 1).$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. $x=u+v$, $y=3u^{2}$, $z=u-v$; $(2,3,0).$
$3x - y + 3z = 3.$
Determine a área da superfície $z=\frac{2}{3}(x^{3/2}+y^{3/2})$, $0\leq x \leq 1$ e $0\leq y\leq 1.$
$\dfrac{4}{15}(3^{5/2} - 2^{7/2} + 1).$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(u-v,u^{2}+v^{2},uv)$, no ponto ${\bf r}(1,1).$
Temos que ${\bf r}(u,v)=\underbrace{(u-v)}_{x(u,v)}\,{\bf i}+\underbrace{(u^{2}+v^{2})}_{y(u,v)}\,{\bf j}+\underbrace{uv}_{z(u,v)}\,{\bf k}$
Primeiro, vamos calcular os vetores tangentes:
$$\begin{array}{rcl}{\bf r}_{u}&=&\frac{\partial x(u,v)}{\partial u}\,{\bf i}+\frac{\partial y(u,v)}{\partial u}\,{\bf j}+\frac{\partial z(u,v)}{\partial u}\,{\bf k}\\&=& \,{\bf i}+2u\,{\bf j}+v\,{\bf k}\end{array}$$
e
$$\begin{array}{rcl}{\bf r}_{v}&=&\frac{\partial x(u,v)}{\partial v}\,{\bf i}+\frac{\partial y(u,v)}{\partial v}\,{\bf j}+\frac{\partial z(u,v)}{\partial v}\,{\bf k}\\&=& -\,{\bf i}+2v\,{\bf j}+u\,{\bf k}\end{array}$$
Assim, o vetor normal ao plano tangente é:
$$\begin{array}{rcl}{\bf r}_{u}\times {\bf r}_{v}&=&\left|\begin{array}{ccc}{\bf i}& {\bf j}&{\bf k}\\1 & 2u & v\\-1 & 2v & u\\\end{array}\right|\\&=&(-2u^{2}-2v^{2})\,{\bf i}-(u+v)\,{\bf j}+(2u+2v)\,{\bf k}\end{array}$$
Como $u=1$ e $v=1$ temos que o vetor normal é $-4\,{\bf i}-2\,{\bf j}+4\,{\bf k}.$
Portanto, uma equação do plano tangente no ponto ${\bf r}(1,1)=(0,2,1)$ é
$$-4\cdot(x-0)-2\cdot(y-2)+4\cdot (z-1)=0$$
$$-4x-2y+4+4z-4=0$$
$$-4x-2y+4z=0 \mbox{ou} 2x+y-2z=0$$
Determine uma representação paramétrica para a superfície descrita a seguir. A superfície cortada do cilindro parabólico $z=4-y^{2}$ pelos planos $x=0$, $x=2$ e $z=0.$
$x = u,$ $y = v,$ $z = 4 - v^2,$ onde $0\leq u \leq 2$ e $-2 \leq v \leq 2.$
Seja $S$ a parte do cone $x^{2}=y^{2}+z^{2}$ que está dentro do cilindro $x^{2}+y^{2}=a^{2}$ e no primeiro octante. Determine a área da superfície $S.$
$\dfrac{\pi a^2}{4}$.
Encontre a massa da lâmina descrita como sendo a porção do parabolóide \(2z=x^2+y^2\) que fica dentro do cilindro \(x^2+y^2=8\) e tem densidade \(\delta_0\) constante.
Identifique a superfície que tem equação paramétrica ${\bf r}(u,v)=2\,\sin u\,{\bf i}+3\,\cos u\,{\bf j}+v\,{\bf k}$, $0\leq v\leq 2.$.
$\dfrac{x^2}{4} + \dfrac{y^{2}}{9} = 1,$ com $0\leq z \leq 2.$
Encontre a massa da lâmina descrita como sendo a porção do cilindro circular \(x^2+z^2=4\) que fica diretamente acima do retângulo \(\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq x\leq 1,\ 0\leq y\leq 4\}\) e tem densidade \(\delta_0\) constante.
\(\dfrac{4}{3}\pi\delta_0\)
Determine uma representação paramétrica para a superfície descrita a seguir. A parte da esfera $x^{2}+y^{2}+z^{2}=4$ que está acima do cone $z=\sqrt{x^{2}+y^{2}}.$
$x = 2\sin(\phi)\cos(\theta),$ $y = 2\sin(\phi)\sin(\theta),$ $z = 2\cos(\phi),$ onde $0\leq \phi \leq \frac{\pi}{4}$ e $0 \leq \theta \leq 2\pi.$
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$, $(u,v)\in \mathbb{R}^{2}.$.
Paraboloide de rotação $z = x^2 + y^2.$
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,\sqrt{1-u^{2}-v^{2}},v)$, $u^{2}+v^{2}\leq 1.$
Semi superfície esférica $x^2 + y^2 + z^2 = 1,$ $y \geq 0.$
Determine se os pontos $P(7,10,4)$ e $Q(5,22,5)$ estão na superfície ${\bf r}(u,v)=(2u+3v,1+5u-v,2+u+v)$.
$P$ não está na superfície; $Q$ está na superfície.
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,1-u^{2})$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$
${\bf r}(u,v)=(u,v,1-u^{2})$, $u\geq 0$,\, $v\geq 0$ e $u+v\leq 1.$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(\arctan (uv),e^{u^{2}-v^{2}},u-v)$, no ponto ${\bf r}(1,-1).$
$(x,y,z) = \left(-\dfrac{\pi}{4},1,2\right) + s\left(-\dfrac{1}{2},2,1\right) + t\left(\dfrac{1}{2},2,-1\right),$ $s,t \in \mathbb{R}.$
Calcule a área da parte da superfície cilíndrica $z^{2}+x^{2}=4$ que se encontra dentro do cilindro $x^{2}+y^{2}\leq 4$ e acima do plano $xy.$
$16.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,1-u-v)$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\dfrac{\sqrt{3}}{2}.$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. $x=u^{2}$, $y=v^{2}$, $z=uv$; $u=1$, $v=1.$
$x + y - 2z = 0.$
Encontre a área da superfície $z=1+3x+3y^{2}$ que está acima do triângulo com vértices $(0,0)$, $(0,1)$ e $(2,1).$
$\dfrac{1}{54}\left(46\sqrt{46} - 10\sqrt{10} \right).$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte do hiperboloide $x^{2}+y^{2}-z^{2}=1$ que está à direita do plano $xz.$
$x =u,$ $z = v,$ $y = \sqrt{1 - u^2 + v^2}.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,4-u^{2}-v^{2})$, $(u,v)\in K$, onde $K$ é o conjunto no plano $uv$ limitado pelo eixo $u$ e pela curva (em coordenadas polares) $\rho=e^{-\theta}$,$0\leq \theta \leq \pi.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\displaystyle \dfrac{1}{72} \left( \ln\left(3\dfrac{\sqrt{e^{2\pi} + 4} + e^{\pi}}{\sqrt{e^{2\pi} + 4} - e^{\pi}} \right) + 3 \ln\left(\dfrac{\sqrt{5} - 1 }{\sqrt{5} + 1 }\right) - 8e^{3\pi} \sqrt{e^{2\pi} + 4}(e^{2\pi} + 1) + 16\sqrt{5} - 6\pi \right).$
Determine uma representação paramétrica para a superfície descrita a seguir. A porção no primeiro octante do cone $z=\sqrt{x^{2}+y^{2}}/2$ entre os planos $z=0$ e $z=3.$
$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = \dfrac{r}{2},$ onde $0 \leq r \leq 6$ e $0\leq \theta \leq \dfrac{\pi}{2}.$
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(v\,\cos u,v\sin u,v)$, $0\leq u\leq 2\pi$,\, $0\leq v \leq h$, onde $h>0$ é um real dado.
Face lateral do cone $\sqrt{x^{2} + y^{2}} \leq z \leq h$.
Seja $f:K\rightarrow \mathbb{R}$ de classe $C^{1}$ no compacto $K$ com fronteira de conteúdo nulo e interior não-vazio. Mostre que a área da superfície $z=f(x,y)$ (isto é, da superfície ${\bf r}$ dada por $x=u$, $y=v$ e $z=f(u,v)$) é dada pela fórmula
$$\iint\limits_{ K}\sqrt{1+\bigg(\frac{\partial f}{\partial x}\bigg)^{2}+\bigg(\frac{\partial f}{\partial y}\bigg)^{2}}dxdy.$$
Encontre a área da parte da esfera $x^{2}+y^{2}+z^{2}=a^{2}$ que está dentro do cilindro $x^{2}+y^{2}=ax.$
$2a^2 (\pi - 2).$
Faça uma correspondência entre as equações e os gráficos identificados a seguir, enumerador respectivamente por $I-VI$, e justifique sua resposta. Determine quais famílias de curvas da grade têm $u$ constante e quais têm $v$ constante.
${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+v{\bf k}.$
${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+\sin u{\bf k}$, $-\pi\leq u\leq \pi.$
${\bf r}(u,v)=\sin v{\bf i}+\cos u\sin 2v{\bf j}+\sin u\sin 2v{\bf k}.$
$x=(1-u)(3+\cos v)\cos 4\pi u$, $y=(1-u)(3+\cos v)\sin 4\pi u$,$z=3u+(1-u)\sin v.$
$x=\cos^{3}u\cos^{3}v$, $y=\sin^{3}u\cos^{3}v$, $z=\sin^{3}v.$
$x=(1-|u|)\cos v$, $y=(1-|u|)\sin v$, $z=u.$
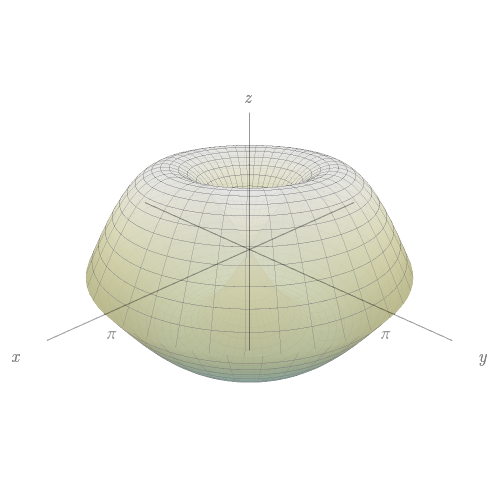
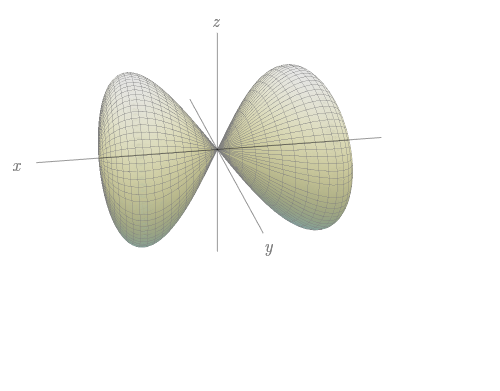
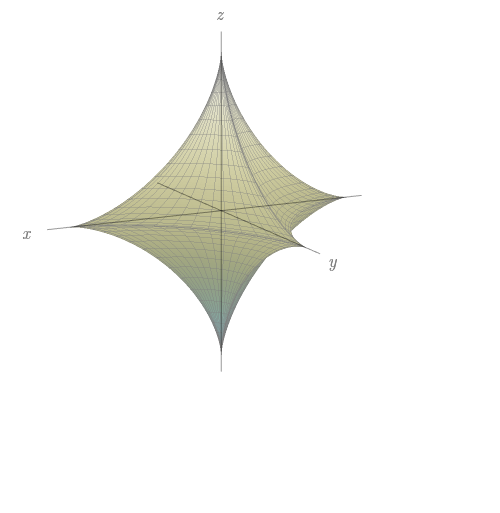
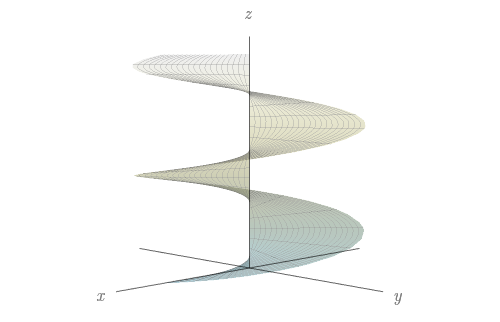
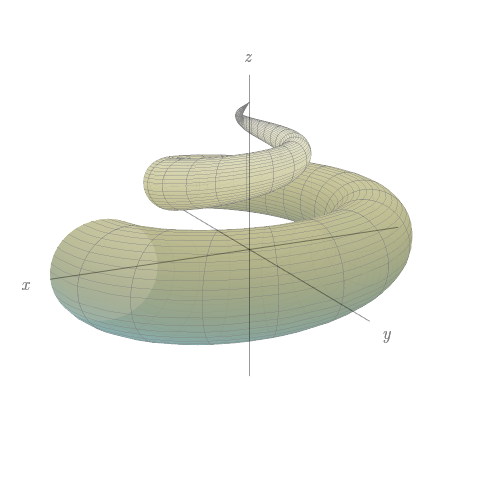
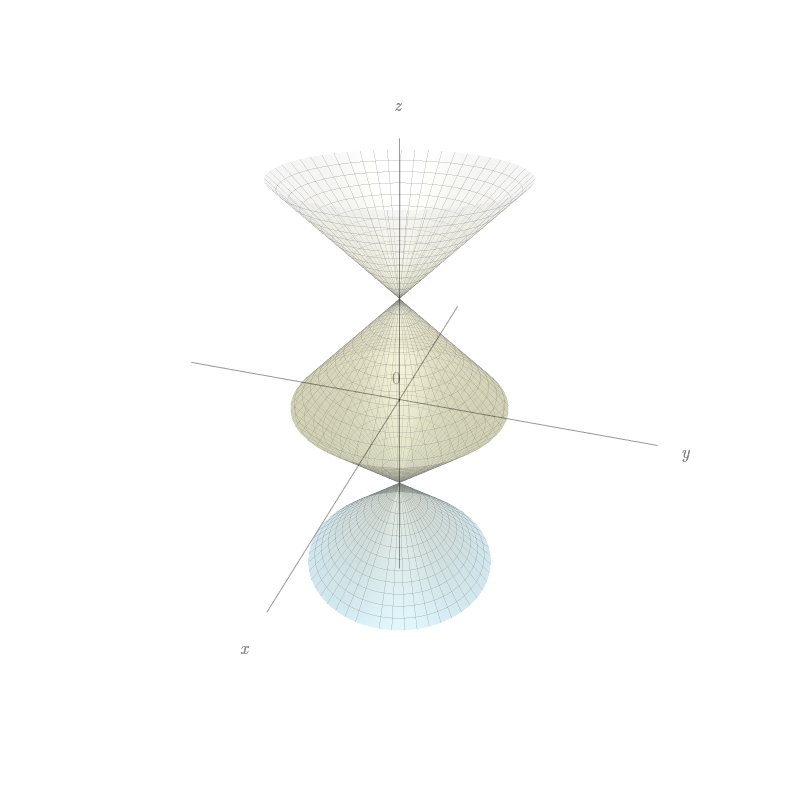
- IV.
- I.
- II.
- V.
- III.
- VI
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(1,u,v)$, $0\leq u\leq 1$, $0\leq v \leq 1.$
Região quadrada do plano $x = 1:$ $0 \leq y \leq 1$ e $0 \leq z \leq 1.$
Determine se os pontos $P(3,-1,5)$ e $Q(-1,3,4)$ estão na superfície ${\bf r}(u,v)=(u+v,u^{2}-v,u+v^{2})$.
$P$ está na superfície; $Q$ não está na superfície.
Determine a área da superfície dada pela parte da superfície $y=4x+z^{2}$ que está entre os planos $x=0$, $x=1$, $z=0$ e $z=1.$
$\dfrac{\sqrt{21}}{2} + \dfrac{17}{4} \left( \ln(2 + \sqrt{21}) - \ln(\sqrt{17}) \right).$
Determine uma representação paramétrica para a superfície descrita a seguir. A porção do cilindro $(x-2)^{2}+z^{2}=4$ entre os planos $y=0$ e $y=3.$
$x = 4\cos^{2}(v),$ $y = u,$ $z = 4\cos(v)\sin(v),$ onde $-\dfrac{\pi}{2}\leq v \leq \dfrac{\pi}{2}$ e $0 \leq u \leq 3.$
Determine a área da superfície dada pela parte do plano $x+2y+z=4$ que está dentro do cilindro $x^{2}+y^{2}=4$.
$4\sqrt{6}\pi.$
Determine uma representação paramétrica para a superfície descrita a seguir. O paraboloide $z=9-x^{2}-y^{2}$, $z\geq 0.$
$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = 9 - r^2,$ onde $0 \leq r \leq 3$ e $0\leq \theta \leq 2\pi.$
Determine uma representação paramétrica para a superfície descrita a seguir. O paraboloide $z=x^{2}+y^{2}$, \, $z\leq 4.$
$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = r^2,$ onde $0 \leq r \leq 2$ e $0\leq \theta \leq 2\pi.$

