Teorema de Green
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}\dfrac{-y}{x^2+y^2} \, dx + \dfrac{ x}{x^2+y^2} \, dy$, $C$ curva fechada, $C^1$ por partes, simples e fronteira de um conjunto $B$ cujo interior contém o círculo $x^2 + y^2 \leq 1$. (Sugestão: Aplique o Teorema de Green à região $K$ compreendida entre a curva $C$ e a circunferência.)
$2\pi.$
Calcule a integral de linha $\displaystyle\oint_{C} xy \, dx + x^2y^3 \, dy$, $C$ é o triângulo com vértices $(0,0)$, $(1,0)$ e $(1,2)$ por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$\dfrac{2}{3}.$
Seja $D$ a região limitada por um caminho fechado e simples $C$ no plano $xy$. As coordenadas do centroide $(\bar{x},\bar{y})$ de $D$ são
$$\bar{x} = \dfrac{1}{2A}\oint_{C}x^2 \, dy \quad \quad\quad\quad \bar{y} = -\dfrac{1}{2A}\oint_{C}y^2 \, dx,$$
em que $A$ é a área de $D$. Encontre o centroide de um quarto de uma região circular de raio $a$.
$\displaystyle \left(\frac{4a}{3\pi},\frac{4a}{3\pi} \right),$ se a região for a parte do disco $x^{2} + y^{2} = a^{2}$ no primeiro quadrante.
Calcule a integral de linha $\displaystyle\oint_{C} xy \, dx + x^2 \, dy$, $C$ é o retângulo com vértices $(0,0)$, $(3,0)$, $(3,1)$ e $(0,1)$ por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$\dfrac{9}{2}.$
Calcule
$$\oint_{C} \dfrac{-y}{x^2+y^2} \, dx + \dfrac{x}{x^2 + y^2} \, dy,$$
em que $C$ é a curva
Podemos escrever $C$ como $C_1 \cup C_2$, em que $C_1$ e $C_2$ são as curvas dadas abaixo.
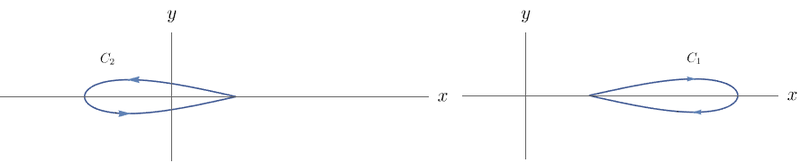
Seja $A$ um aberto simplesmente conexo que contém $C_1$ e não contém a origem. O campo $\mathbf{F}$ restrito a $A$ é conservativo, pois $A$ é aberto e simplesmente conexo, $P(x,y) = \dfrac{-y}{x^2 + y^2}$ e $Q(x,y) = \dfrac{x}{x^2 + y^2}$ possuem derivadas de primeira ordem contínuas em $A$ e $P$ e $Q$ satisfazem a relação $\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}$. Então,
$$\oint_{C_1}\mathbf{F} \cdot\, d\mathbf{r} = 0.$$
Não podemos proceder de maneira análoga em $C_2$, já que todo aberto $B$ que contém a curva $C_2$ e não contém a origem não será simplesmente conexo. Com isso, não conseguimos garantir que o campo $\mathbf{F}$ restrito a $B$ é conservativo (observe que, a princípio, não podemos afirmar que o campo é não conservativo).
A ideia para contornar esse problema é ``isolar" a origem com uma curva fechada $C_3$, a princípio arbitrária. Vamos escolher essa curva $C_3$ de maneira conveniente para que consigamos resolver o problema. Seja $\varepsilon > 0$ pequeno o suficiente para que a curva $C_3$ parametrizada por $r(t) = (\varepsilon \cos{t}, \varepsilon \sin{t})$, com $t$ variando de $2\pi$ a $0$, não intercepte a curva $C_2$ e esteja entre a curva $C_2$ e a origem.
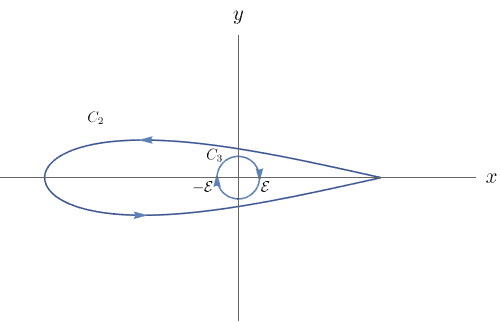
Considere $D_1 = \{(x,y) \in \mathbb{R}^2: (x,y) \mbox{ está entre } C_2 \mbox{ e } C_3 \mbox{ e } y \geq 0\}$ e $D_2 = \{(x,y) \in \mathbb{R}^2: (x,y) \mbox{ está entre } C_2 \mbox{ e } C_3 \mbox{ e } y \leq 0\}$. As curvas que delimitam $D_1$ e $D_2$ são $C_{D_1}= C_{2}^+\cup C_{a}\cup C_{3}^+\cup C_{b}$ e $C_{D_2}=C_{2}^-\cup -C_{b}\cup C_{3}^- \cup -C_{a}$, respectivamente, e estão ilustradas a seguir.
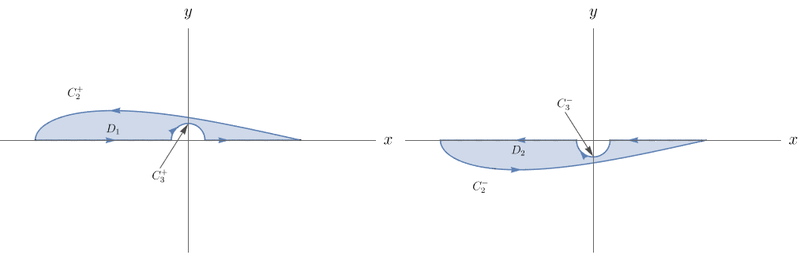
Note que
$$\oint_{C_{D_1}} \mathbf{F} \cdot d\mathbf{r} = \int_{C^+_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C_a} \mathbf{F} \cdot d\mathbf{r} + \int_{C^+_3} \mathbf{F} \cdot d\mathbf{r} + \int_{C_b} \mathbf{F} \cdot d\mathbf{r} \qquad (\star)$$
e
$$\oint_{C_{D_2}} \mathbf{F} \cdot d\mathbf{r} = \int_{C^-_2} \mathbf{F} \cdot d\mathbf{r} + \int_{-C_a} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_3} \mathbf{F} \cdot d\mathbf{r} + \int_{-C_b} \mathbf{F} \cdot d\mathbf{r} \qquad (\star \star).$$
Como $\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}$, temos, pelo Teorema de Green,
$$\displaystyle\oint_{C_{D_1}} \mathbf{F} \cdot d\mathbf{r} = \iint\limits_{D_1} 0 \, dA = 0$$
e
$$\displaystyle\oint_{C_{D_2}} \mathbf{F} \cdot d\mathbf{r} = \iint\limits_{D_2} 0 \, dA = 0.$$
Somando as equações ($\star$) e ($\star \star$), obtemos
$$\int_{C^+_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C^+_3} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_3} \mathbf{F} \cdot d\mathbf{r} = 0,$$
isto é,
$$\int_{C_2} \mathbf{F} \cdot d\mathbf{r} = -\int_{C_3} \mathbf{F} \cdot d\mathbf{r} = \int_{-C_3} \mathbf{F} \cdot d\mathbf{r}.$$
Assim, basta determinar $\int_{-C_3} \mathbf{F} \cdot d\mathbf{r}$. A parametrização de $-C_3$ é $r(t) = (\varepsilon \cos{t}, \varepsilon \sin{t})$, com $t$ variando de $0$ a $2\pi$. Daí,
$$\begin{array}{rcl}\displaystyle \int_{-C_3} \mathbf{F} \cdot d\mathbf{r} & = & \displaystyle \int_{0}^{2\pi} \left(\frac{-\varepsilon \sin{t}}{\varepsilon^2},\frac{\varepsilon \cos{t}}{\varepsilon^2}\right) \cdot (-\varepsilon \sin{t}, \varepsilon \cos{t}) \, dt \\& = & \displaystyle \int_{0}^{2\pi} 1 \, dt = 2\pi.\end{array}$$
Portanto,
$$\oint_{C} \mathbf{F} \cdot d\mathbf{r} = \oint_{C_1} \mathbf{F} \cdot d\mathbf{r} + \oint_{C_2} \mathbf{F} \cdot d\mathbf{r} = 0 + 2\pi = 2\pi.$$
Calcule a área da região $R$ delimitada pela cardioide $\mathbf{r}(t) = (x(t),y(t))$, em que $x(t) = 2\cos{t}-\cos{2t}$ e $y(t) = 2\sin{t}-\sin{2t}$, $t \in [0,2\pi]$.
$6\pi.$
Use o Teorema de Green para achar o trabalho realizado pela força $\mathbf{F}(x,y) = x(x+y)\mathbf{i} + xy^2\mathbf{j}$ ao mover uma partícula da origem ao longo do eixo $x$ até $(1,0)$, em seguida ao longo de um segmento de reta até $(0,1)$ e então de volta à origem ao longo do eixo $y$.
$-\dfrac{1}{12}.$
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (\sqrt{x} + y^3,x^2+\sqrt{y})$, $C$ consiste no arco da curva $y = \sin{x}$ de $(0,0)$ a $(\pi,0)$ e no segmento de reta $(\pi,0)$ a $(0,0)$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$\dfrac{4}{3} - 2\pi.$
Calcule $\int_{C}\mathbf{F}\cdot\, d\mathbf{r}$, em que
$$\mathbf{F}(x,y) = (x^2+y)\mathbf{i} + (3x-y^2)\mathbf{j}$$
e $C$ é a fronteira orientada positivamente de uma região $D$ que tem área 6.
$12.$
Se $C$ é o segmento de reta ligando o ponto $(x_1,y_1)$ ao ponto $(x_2,y_2)$, mostre que
$$\int_{C}x \, dy - y \, dx = x_1y_2-x_2y_1.$$
Se os vértices de um polígono, na ordem anti-horária, são
$$ (x_1,y_1), (x_2,y_2), \ldots, (x_n,y_n), $$
mostre que a área do polígono é
$$A=\dfrac{1}{2}[(x_1y_2-x_2y_1) + (x_2y_3-x_3y_2) + \cdots + (x_{n-1}y_n - x_ny_{n-1}) + (x_ny_1-x_1y_n)].$$
Determine a área do pentágono com vértices $(0,0)$, $(2,1)$, $(1,3)$, $(0,2)$ e $(-1,1)$.
Use as equações paramétricas do segmento de reta: $x = (1-t)x_{1} + tx_{2}$ e $y = (1-t)y_{1} + ty_{2},$ $0 \leq t \leq 1.$
Aplique o Teorema de Green ao caminho $C = C_{1} \cup C_{2} \cup \cdots \cup C_{n},$ onde $C_{i}$ é o segmento ligando o ponto $(x_{i},y_{i})$ ao ponto $(x_{i + 1},y_{i + 1}),$ para cada $i = 1,\cdots, n-1.$
$\dfrac{9}{2}.$
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas para o caso em que $f(x,y) = 1$:
$$\iint\limits_{R} dxdy = \iint\limits_{R}\left|\dfrac{\partial(x,y)}{\partial(u,v)}\right|\, dudv.$$
Aqui, $R$ é a região do plano $xy$ que corresponde à região $S$ do plano $uv$ sob a transformação dada por $x=g(u,v)$, $y=h(u,v)$. (Sugestão: observe que o lado esquerdo é $A(R)$. Converta a integral de linha sobre $\partial R$ para uma integral de linha sobre $\partial S$ e aplique o Teorema de Green no plano $uv$.)
Dica: pelo Teorema de Green, $A(R) = \displaystyle \iint_{R} dxdy = \int_{\partial R} x dy.$ Escolhendo a orientação positiva em $\partial S$ correspondente a orientação positiva em $\partial R,$ segue que
$$\displaystyle \int_{\partial R} x dy = \int_{\partial S} g(u,v) \dfrac{\partial h}{\partial u} du + g(u,v) \frac{\partial h}{\partial v} dv.$$
Conclua utilizando o Teorema de Green no plano $uv$ e a Regra da Cadeia.
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C} \sin{y} \, dx + x\cos{y} \, dy$, $C$ é a elipse $x^2 + xy + y^2 = 1$.
$0.$
Use o Teorema de Green para determinar o trabalho realizado pelo campo de forças \(\displaystyle\mathbf{F}(x,y)=\sqrt{y}\textbf{i}+\sqrt{x}\textbf{j}\) sobre uma partícula que percorre uma vez, no sentido anti-horário, a curva fechada dada pelas equações \(y=0\), \(x=2\) e \(y=x^3/4\).
Demonstre que se $R$ é uma região no plano limitada por uma curva $C$ simples, fechada e suave por partes, então a área de $R$, denotada por $A(R)$, pode ser dada por
$$\oint_{C}x\, dy,$$
em que a curva está orientada no sentido positivo.
Temos que
$$A(R) = \iint\limits_{R} 1 \, dA.$$
A fim de utilizar o Teorema de Green, devemos encontrar funções $P$ e $Q$ que tenham derivadas de primeira ordem contínuas em um aberto que contenha a curva $C$ e o interior de $C$ e que satisfaçam a relação $\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 1$. Observe que a curva $C$ já satisfaz as hipóteses desse teorema e $C$ é a fronteira de $R$. Um exemplo de funções $P$ e $Q$ é $P(x,y) = 0$ e $Q(x,y) = x$. Portanto, pelo Teorema de Green,
$$\iint\limits_{R} 1 \, dA = \oint_{C}0 \, dx + x\, dy = \oint_{C}x\, dy.$$
Calcule a integral de linha $\displaystyle\oint_{C} (x-y) dx + (x+y)dy$, $C$ é o círculo com centro na origem e raio 2, por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$8\pi.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
$\displaystyle\int_{C}y^3 \, dx - x^3 \, dy$, $C$ é o círculo $x^2 + y^2 = 4$.
Observe que a curva $C$ com orientação positiva está nas hipóteses do Teorema de Green, assim como o campo $\mathbf{F}(x,y) = (y^3, -x^3)$. Logo,
$$\displaystyle\int_{C}y^3 \, dx - x^3 \, dy = \iint\limits_{D} \left(\frac{\partial}{\partial x}(-x^3) - \frac{\partial}{\partial y}(y^3)\right) \, dA = -3 \iint\limits_{D} (x^2 + y^2) \, dA,$$
em que $D = \{(x,y) \in \mathbb{R}^2: x^2 + y^2 \leq 4\}$. Usando coordenadas polares
$$\begin{cases}x = r \cos{\theta} \\y = r \sin{\theta}, \\\end{cases}$$
temos que a região de integração $D$ pode ser escrita como $$\{(r,\theta) \in \mathbb{R}^2: 0 \leq r \leq 2, 0 \leq \theta \leq 2 \pi\}$$ e o jacobiano dessa mudança de coordenadas é igual a $r$. Logo,
$$\iint\limits_{ D} (x^2 + y^2) dA = \displaystyle\int_{0}^{2\pi} \int_{0}^{2}r^2 \cdot r\,dr d\theta = 8\pi.$$
Portanto, $\displaystyle\int_{C}y^3 \, dx - x^3 \,dy = -24\pi$.
Se uma circunferência $C$ de raio $1$ rola ao longo do interior da circunferência $x^2+y^2=16$, um ponto fixo $P$ de $C$ descreve uma curva chamada epicicloide, com equações paramétricas $x = 5\cos{t}-\cos{5t}$, $y = 5\sin{t} - \sin{5t}$. Faça o gráfico da epicicloide e calcule a área da região que ela envolve.
$30\pi.$
Se $\mathbf{F}(x,y) = (-y\mathbf{i} + x\mathbf{j})/(x^2+y^2)$, mostre que $\int_{C}\mathbf{F} \cdot d\mathbf{r} = 0$ para todo caminho fechado simples que não passe pela origem e nem a circunde.
Dica: como $C$ é um caminho fechado simples que não passa pela origem e não circunda a origem, então existe uma região aberta $A$ que ainda não contém a origem, mas contém $D,$ a região limitada por $C.$ Em $A,$ tanto $-y/(x^{2} + y^{2})$ quanto $x/(x^{2} + y^{2})$ possuem derivadas parciais contínuas e podemos aplicar o Teorema de Green.
Calcule a área sob um arco da cicloide $x = t-\sin{t}$, $y = 1-\cos{t}$.
Queremos determinar a área da região $R$ mostrada na figura abaixo.
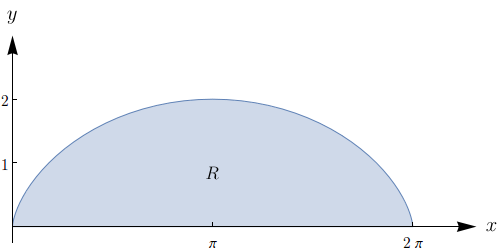
Sabemos que, se $y = f(x)$, então a integral $\int_{a}^{b}f(x)dx$ calcula a área que está abaixo do gráfico de $f$ e acima do eixo $x$, com $x$ variando entre $a$ e $b$. A princípio, poderíamos tentar encontrar uma expressão que relacionasse $x(t)$ e $y(t)$ na parametrização da cicloide, mas esse parece ser um trabalho difícil. Usaremos então o que foi provado no exercício anterior. Temos que
$$A(R) = \oint_{C}x\, dy,$$
em que $C = C_1 \cup C_2$ é a curva descrita na figura a seguir.
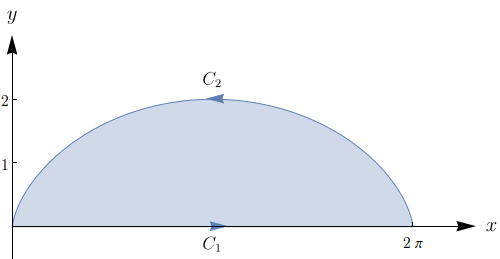
Uma parametrização de $C_1$ é $r_1(t) = (x_1(t),y_1(t)) = (t,0)$, em que $0 \leq t \leq 2\pi$. Nesse caso, $y_1'(t) = 0$. Logo,
$$\oint_{C_1}x\, dy = \int_{0}^{2\pi}(t)(0)\, dt = 0.$$
Uma parametrização de $C_2$ é $r_2(t) = (x_2(t),y_2(t)) = (t-\sin{t},1-\cos{t})$, em que $t$ varia de $2\pi$ a $0$. Nesse caso, $y_2'(t) = \sin{t}$. Logo,
$$\begin{array}{rcl}\displaystyle \oint_{C_2}x\, dy & = & \displaystyle \int_{2\pi}^{0}(t-\sin{t}) (\sin{t})\, dt \\ & = & \displaystyle \int_{0}^{2\pi}(\sin^2{t} - t\sin{t}) \, dt \\ & = & \displaystyle \int_{0}^{2\pi}\frac{1-\cos(2t)}{2}\, dt - \int_{0}^{2\pi}t\sin{t} \, dt \\ & = & \pi + 2\pi = 3\pi.\end{array}$$
Portanto, a área da região é $3\pi$.
(Observe que, para resolver a integral $\int_{0}^{2\pi}t\sin{t} \, dt$, usamos integração por partes com $u=t$ e $dv=\sin{t}\,dt$.)
Seja $D$ a região limitada por um caminho fechado e simples $C$ no plano $xy$. Utilize o Teorema de Green para demonstrar que as coordenadas do centroide $(\bar{x},\bar{y})$ de $D$ são
$$\bar{x} = \dfrac{1}{2A}\oint_{C}x^2 \, dy \quad \quad\quad\quad \bar{y} = -\dfrac{1}{2A}\oint_{C}y^2 \, dx,$$
em que $A$ é a área de $D$.
$\dfrac{1}{2A}\oint_{C}x^2 \, dy = \dfrac{1}{2A} \iint_{D} 2x \, dA = \bar{x}$ e $-\dfrac{1}{2A}\oint_{C}y^2 \, dx = -\dfrac{1}{2A}\iint_{D} (-2y) \, dA = \bar{y}$
Calcule o trabalho realizado pela força $\mathbf{F}(x,y) = xy\mathbf{i}+y^2\mathbf{j}$ ao mover uma partícula da origem ao longo da reta $y=x$ até $(1,1)$ e então de volta à origem ao longo da curva $y=x^2$.
$\dfrac{1}{12}.$
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = 4x^3y^3\mathbf{i} + (3x^4y^2+5x)\mathbf{j}$, $C$ é a fronteira do quadrado de vértices $(-1,0)$, $(0,-1)$, $(1,0)$ e $(0,1)$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$10.$
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (2x+y)\mathbf{i} + (3x-y)\mathbf{j}$, $C$ é uma curva fechada, simples, $C^1$ por partes, orientada no sentido positivo, cuja imagem é a fronteira de um compacto $B$ com área $\alpha$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$2\times$(Área de $B$).
Use o Teorema de Green para determinar o trabalho realizado pelo campo de forças \(\displaystyle\textbf{F}(x,y)=xy\textbf{i}+(\dfrac{1}{2}x^2+xy)\textbf{j}\) sobre uma partícula que se move ao longo do caminho que começa em \((5,0)\), percorre o semicírculo superior \(x^2+y^2=25\) e retorna ao seu ponto de partida ao longo do eixo \(x\).
\(\dfrac{250}{3}\)
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (e^x+x^2y,e^y-xy^2)$, $C$ é a circunferência $x^2+y^2=25$, orientada no sentido horário. (Verifique a orientação da curva antes de aplicar o Teorema.)
$\dfrac{625\pi}{2}.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}(y+e^{\sqrt{x}}) \, dx + (2x+\cos{y^2}) \, dy$, $C$ é a fronteira da região englobada pelas parábolas $y=x^2$ e $x=y^2$.
$\dfrac{1}{3}.$
Calcule a área da região limitada pela elipse $x = a\cos{t}$, $y=b\sin{t}$, $0\leq t \leq \pi/2$, em que $a > 0$ e $b > 0$.
$\pi ab.$
Determine o trabalho $W = \int_{C}\mathbf{F}\cdot\, d\mathbf{r}$ realizado pelo campo de força
$$\mathbf{F}(x,y) = x\mathbf{i} + (x^3 + 3xy^2)\mathbf{j}$$
em uma partícula que inicialmente está no ponto $(-2,0)$, se move ao longo do eixo $x$ para $(2,0)$ e então se move ao longo da semicircunferência $y = \sqrt{4-x^2}$ até o ponto inicial.
$12\pi.$
Calcule a área da região limitada pela astroide $x=\cos^3{t}$, $y = \sin^3{t}$, $0 \leq t \leq 2\pi$.
$\dfrac{3\pi}{8}.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}e^y \, dx + 2xe^y \, dy$, $C$ é o quadrado de lados $x=0$, $x=1$, $y=0$ e $y=1$.
$e - 1.$