Derivadas parciais
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=1+xy^{2}-2z^{2}$.
$\displaystyle f_{x} = 1+ y^{2} ,\;\;\;\; f_{y} = 2xy \;\;\;\;\text{e}\;\;\;\; f_{z} = -4z$.
Determine as derivadas parciais de primeira ordem da função $f(r,s)=r\ln(r^{2}+s^{2})$.
Sendo $f(r,s)=r\cdot \ln(r^{2}+s^{2})$, temos que as derivadas parciais em relação a $r$ e $s$, respectivamente, são:
$\bullet f_{r}(r,s)=1\cdot \ln(r^{2}+s^{2})+r\cdot \dfrac{1}{r^{2}+s^{2}}\cdot 2r=\ln(r^{2}+s^{2})+\dfrac{2r^{2}}{r^{2}+s^{2}}.$
$\bullet f_{s}(r,s)=0\cdot \ln(r^{2}+s^{2})+r\cdot \dfrac{1}{r^{2}+s^{2}}\cdot 2s=\dfrac{2rs}{r^{2}+s^{2}}.$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=e^{-x}\;\sin(x+y)$.
$\displaystyle \frac{\partial f}{\partial x} = -e^{-x} \sin(x + y) + e^{-x}\cos(x + y) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = e^{-x}\cos(x + y)$.
Determine as derivadas parciais de primeira ordem da função $f(x,y)=\dfrac{x-y}{x+y}$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{2y}{(x + y)^{2}}\;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = -\frac{2x}{(x + y)^{2}}$.
Determine a derivada parcial $f_{x}(3,4)$, onde $f(x,y)=\ln(x+\sqrt{x^{2}+y^{2}}).$
$f_{x}(3,4) = \frac{1}{5}$.
Verifique que a função $u=1/\sqrt{x^{2}+y^{2}+z^{2}}$ é uma solução da equação de Laplace tridimensional $u_{xx}+u_{yy}+u_{zz}=0.$
$\displaystyle u_{xx} = \frac{2x^{2} - y^{2} - z^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}},\;\;\; u_{yy} = \frac{2y^{2} - x^{2} - z^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}}\;\;\;\text{e}\;\;\;u_{zz} = \frac{2z^{2} - x^{2} - y^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}}$.
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $g(x,y)=4x^{3}y^{4}+y^{3}$.
$\displaystyle \frac{\partial^{2} g}{\partial x^{2}}= 24xy^{2},\;\;\;\;\; \frac{\partial^{2} g}{\partial y^{2}}= 48x^{3} y^{2} \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} g}{\partial x\partial y}= \frac{\partial^{2} g}{\partial y\partial x}= 48x^{2}y^{3}.$
Determine as derivadas parciais de $f(x,y)=\sqrt[3]{x^{3}+y^{2}+3}$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{x^{2}}{\sqrt[3]{(x^{3} + y^{3} + 3)^{2}}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = \frac{2y}{3 \sqrt[3]{(x^{3} + y^{3} + 3)^{2}}} .$
Considere a função $z=\dfrac{xy^{2}}{x^{2}+y^{2}}.$ Verifique que $x\dfrac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=z.$
$\displaystyle \frac{\partial z}{\partial x} = \frac{y^{4} - x^{2}y^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{3}y}{(x^{2} + y^{2})^{2}}.$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=\cos^{2}(3x-y^2)$.
$\displaystyle \frac{\partial f}{\partial x} = -6\cos (3x - y^{2}) \sin(3x - y^{2}) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = 4y \cos (3x - y^{2}) \sin(3x - y^{2})$.
Determine as derivadas parciais de $f(x,y)=5x^{4}y^{2}+xy^{3}+4$.
$\displaystyle \frac{\partial f}{\partial x} = 20x^{3}y^{2} + y^{3}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 10x^{4}y + 3xy^{2}.$
O índice de sensação térmica $W$ é a temperatura sentida quando a temperatura real é $T$ e a velocidade do vento, $v$. Portanto, podemos escrever $W=f(T,v)$. Considerando a tabela abaixo:
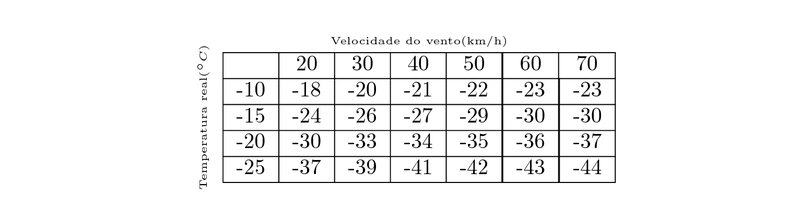
Estime os valores de $f_{T}(-15,30)$ e $f_{v}(-15,30)$. Quais são as nterpretações práticas desses valores?
Em geral, o que se pode dizer sobre o sinal de $\partial W/\partial T$ e $\partial W/\partial v$?
Qual parece ser o valor do seguinte limite
$$\lim_{v\rightarrow \infty}\frac{\partial W}{\partial v}?$$
$f_{T}(-15,30) \approx 1.3$ Isto significa que quando a temperatura real é $-15º$C e a velocidade do vento é $30$km/h, a temperatura aparente aumenta cerca de $1.3º$C para cada $1º$C que a temperatura real aumenta;\\
$f_{v}(-15,30) \approx -0.15$ Isto significa que quando a temperatura real é $-15º$C e a velocidade do vento é $30$km/h, a temperatura aparente diminui cerca de $0.15º$C para cada $1$km/h que a velocidade do vento aumenta.
$\frac{\partial W}{\partial T} > 0$ e $\frac{\partial W}{\partial v} \leq 0.$
$\lim_{v \to \infty} \frac{\partial W}{\partial v} = 0.$
Determine a derivada parcial indicada. $u=e^{r\theta}\sin{\theta}$; $\dfrac{\partial ^{3}u}{\partial r^{2}\partial \theta}$.
$\dfrac{\partial ^{3}u}{\partial r^{2}\partial \theta} = \theta e^{r\theta} (2\sin \theta + \theta \cos \theta + r\theta \sin \theta)$.
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função de uma variável real, diferenciável e tal que $\phi '(1)=4.$ Seja $g(x,y)=\phi\bigg(\dfrac{x}{y}\bigg).$ Verifique que, para todo $(x,y)\in \mathbb{R}^{2}$, com $y\neq 0$, temos que
$$x\;\dfrac{\partial g}{\partial x}(x,y)+y\;\dfrac{\partial g}{\partial y}(x,y)=0.$$
São mostradas as curvas de nível de uma função $f.$ Determine se as seguintes derivadas parciais são positivas ou negativas no ponto $P.$
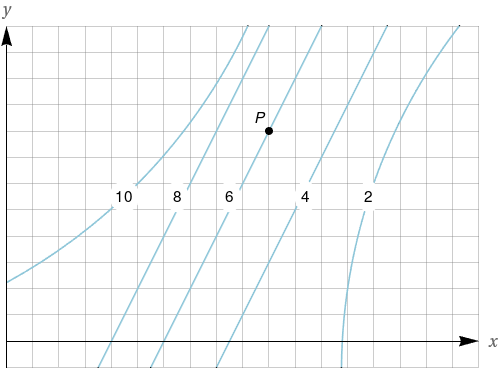
$f_{x}$
$f_{xx}$
$f_{yy}$$f_{y}$
$f_{xy}$
Negativa
Positiva
Positiva
Negativa
Positiva
Determine as derivadas parciais de primeira ordem da função $u=x^{y/z}$.
$\displaystyle \frac{\partial u}{\partial x} = \frac{y}{z} x^{(y/z) - 1},\;\;\; \frac{\partial u}{\partial y} = x^{y/z} \ln x \;\;\;\text{e}\;\;\; \frac{\partial u}{\partial z} = - \frac{yx^{y/z}}{z^{2}} \ln x$.
Determine as derivadas parciais de $z=(x^{2}+y^{2})\ln(x^{2}+y^{2})$.
$\displaystyle \frac{\partial z}{\partial x} = 2x(1 + \ln(x^{2} + y^ {2}))\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = 2y(1 + \ln(x^{2} + y^ {2})).$
Determine as derivadas parciais de $z=\arctan \dfrac{x}{y}$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{y}{x^{2} + y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{-x}{x^{2} + y^{2}}.$
As seguintes superfícies, rotuladas $a$, $b$ e $c$ de cima para baixo, são gráficos de uma função $f$ e de suas derivadas parciais $f_{x}$ e $f_{y}$. Identifique cada superfície e dê razões para sua escolha.
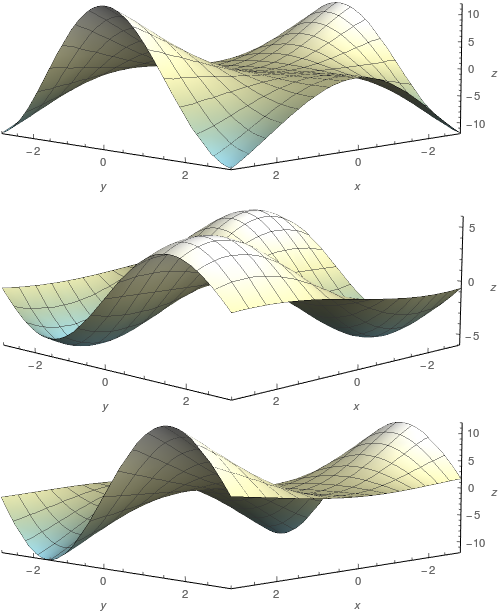
a) $f_{y},$ b) $f_{x},$ c) $f$.
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $z=e^{x^{2}-y^{2}}$.
$\begin{aligned}[t]\frac{\partial^{2} z}{\partial x^{2}} &= 2e^{x^{2} - y^{2}}(1 + 2x^{2}),\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= 2e^{x^{2} - y^{2}}(2y^{2} - 1) \;\;\;\;\;\text{e}\\\frac{\partial^{2} z}{\partial x\partial y} &= \frac{\partial^{2} z}{\partial y\partial x}= -4xye^{x^{2} - y^{2}}.\end{aligned}$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=(xy-1)^{2}$.
$\displaystyle \frac{\partial f}{\partial x} = 2y(xy - 1)\;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = 2x (xy - 1)$.
Determine as derivadas parciais de $z=\dfrac{x^{3}+y^{2}}{x^{2}+y^{2}}$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{x^{4} + 3x^{2}y^{2} - 2xy^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{2}y(1 - x)}{(x^{2} + y^{2})^{2}}.$
Calcule as derivadas parciais de $s = f(x,y,z,w)$ dada por $s = xw \ln{(x^2 + y^2 + z^2 + w^2)}$.
$\begin{aligned}[t]\frac{\partial s}{\partial x} &= w \left( \frac{2x^{2}}{x^{2} + y^{2} + z^{2} + w^{2}} + \ln (x^{2} + y^{2} + z^{2} + w^{2})\right),\\\frac{\partial s}{\partial y} &= \frac{2xyw}{x^{2} + y^{2} + z^{2} + w^{2}},\;\;\;\; \frac{\partial s}{\partial z} = w \frac{2xzw}{x^{2} + y^{2} + z^{2} + w^{2}}\;\;\;\;\;\text{e}\\\frac{\partial s}{\partial w} &= x \left( \frac{2w^{2}}{x^{2} + y^{2} + z^{2} + w^{2}} + \ln (x^{2} + y^{2} + z^{2} + w^{2})\right).\end{aligned}$
Considere a função
$$f(x,y)=\begin{cases}x+y, & \quad \text{se } xy=0,\\\kappa, & \quad \text{caso contrário},\\\end{cases}$$
em que $\kappa$ é um número real. Determine as derivadas parciais de primeira ordem de $f$ em $(0,0).$
$\displaystyle \frac{\partial f}{\partial x} (0,0) = \frac{\partial f}{\partial y} (0,0) = 1$.
Determine as derivadas parciais indicadas. $w=\dfrac{x}{y+2z}$; \;\;\;\;$\dfrac{\partial^{3}w}{\partial z\partial y \partial x}$, \;\;\;\;$\dfrac{\partial^{3}w}{\partial x^{2}\partial y}$.
$\displaystyle \frac{\partial^{3}w}{\partial z\partial y \partial x} = \frac{4}{(y + 2z)^{3}}\;\;\;\text{e} \;\;\;\; \frac{\partial^{3}w}{\partial x^{2}\partial y} = 0$.
Determine as derivadas parciais de primeira ordem da função $f(x,y)=\displaystyle\int_{y}^{x}\cos^2t \ \mathrm{d}t$.
Sendo $f(x,y)=\displaystyle\int_{y}^{x}\cos (t^{2})\,dt$, temos que as derivadas parciais em relação a $x$ e $y$, respectivamente, são:
$\bullet \dfrac{\partial}{\partial x}f(x,y)=\dfrac{\partial}{\partial x}\bigg(\displaystyle\int_{y}^{x}\cos(t^{2})\bigg)=\cos(x^{2}).$
$\bullet \dfrac{\partial}{\partial y}f(x,y)=\dfrac{\partial}{\partial y}\bigg(\displaystyle\int_{y}^{x}\cos(t^{2})\bigg)=\dfrac{\partial}{\partial y}\bigg(-\displaystyle\int_{x}^{y}\cos(t^{2})\bigg)=-\cos(y^{2}).$
Notemos que nas soluções das derivadas parciais acima utilizamos o Teorema Fundamental do Cálculo.
Determine as derivadas parciais de primeira ordem da função $u=te^{w/t}$.
$\displaystyle \frac{\partial u}{\partial t} = e^{w/t} \left( 1 - \frac{w}{t} \right)\;\;\;\text{e}\;\;\; \frac{\partial u}{\partial w} = e^{w/t}$.
Determine as derivadas parciais de $g(x,y)=x^{y}$.
$\displaystyle \frac{\partial g}{\partial x} = yx^{y - 1}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial g}{\partial y} = x^{y} \ln x.$
Disseram-lhe que existe uma função $f$ cujas derivadas parciais são \[f_{x}(x,y)=x+4y \quad \mbox{e} \quad f_{y}(x,y)=3x-y,\] e cujas derivadas parciais de segunda ordem são contínuas. Você deve acreditar nisso?
Não, pois pelo Teorema de Clairaut deveria ser verdade que $f_{xy} = f_{yx},$ mas temos $f_{xy} = 4 \neq 3 = f_{yx}.$
Determine $\dfrac{ \partial f}{\partial x}$ e $\dfrac{\partial f}{\partial y}$, sendo $f(x,y)= \begin{cases}\dfrac{x+y^{4}}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= \begin{cases}\dfrac{y^{2} - x^{2} - 2xy^{4}}{(x^{2}+y^{2})^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\\text{não existe} & \quad \text{se } (x,y)=(0,0)\\\end{cases} \;\;\;\; \text{e}\\\frac{\partial f}{\partial y} &= \begin{cases}\dfrac{4x^{2}y^{3} + 2y^{5} - 2xy}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}\end{aligned}$
Seja $z=e^{y}\phi(x-y)$, onde $\phi$ é uma função diferenciável de uma variável real. Mostre que $$\dfrac{\partial z}{\partial x}+\dfrac{\partial z}{\partial y}=z.$$
$\displaystyle \frac{\partial z}{\partial x} = e^{y}\phi'(x-y) \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = e^{y} \phi(x-y) -e^{y}\phi' (x-y).$
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função de uma variável real, diferenciável e tal que $\phi '(1)=4.$ Seja $g(x,y)=\phi\bigg(\dfrac{x}{y}\bigg).$ Calcule
$\dfrac{\partial g}{\partial x}(1,1)$.
$\dfrac{\partial g}{\partial y}(1,1)$.
$\displaystyle \frac{\partial g}{\partial x} = \frac{1}{y} \phi'\left( \frac{x}{y} \right)$
$\displaystyle \frac{\partial g}{\partial y} = -\frac{x}{y^{2}} \phi' \left( \frac{x}{y} \right).$
Calcule as derivadas parciais de $w = \dfrac{xyz}{x + y + z}$.
$\displaystyle \frac{\partial w}{\partial x} = \frac{yz(y+z)}{(x+y+z)^{2}},\;\;\;\; \frac{\partial w}{\partial y} = \frac{xz(x+z)}{(x+y+z)^{2}}\;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial w}{\partial z} = \frac{xy(x+y)}{(x+y+z)^{2}}.$
Determine as derivadas parciais de $z=\cos(xy)$.
$\displaystyle \frac{\partial z}{\partial x} = -y\sin(xy)\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = -x\sin(xy).$
Use a definição de derivadas parciais como limites para encontrar $f_{x}(x,y)$ e $f_{y}(x,y)$, sendo $f(x,y)=x^{2}y-x^{3}y$.
$\displaystyle f_{x} = y^{2} - 3x^{2}y \;\;\;\text{e}\;\;\; f_{y} = 2xy - x^{3}$.
Determine $\partial z/\partial x$ e $\partial z/\partial y$, sendo $z=f(x)+g(y)$.
$\displaystyle \frac{\partial z}{\partial x} = f'(x)$
$\frac{\partial z}{\partial y} = g'(y)$.
Calcule as derivadas parciais de $f(x,y,z) = \sin{(x^2 + y^2 + z^2)}$.
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= 2x \cos (x^{2} + y^{2} + z^{2}),\;\;\;\; \frac{\partial f}{\partial y} = 2y \cos (x^{2} + y^{2} + z^{2}) \;\;\;\;\;\text{e}\\\frac{\partial f}{\partial z} &= 2z \cos (x^{2} + y^{2} + z^{2}).\end{aligned}$
Seja $f(x,y)=\dfrac{1}{x^{2}+y^{2}}$. Verifique que
$x\;\dfrac{\partial ^{2}f}{\partial x^{2}}(x,y)+y\;\dfrac{\partial^{2} f}{\partial y \partial x}(x,y)=-3\dfrac{\partial f}{\partial x}(x,y)$
$\dfrac{\partial ^{2}f}{\partial x^{2}}(x,y)+\dfrac{\partial^{2} f}{\partial y^{2}}(x,y)=\dfrac{4}{(x^{2}+y^{2})^{2}}$
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= -\frac{2x}{(x^{2} + y^{2})^{2}},\;\;\;\;\; \frac{\partial^{2} f}{\partial x^{2}}= \frac{6 x^{2} - 2y^{2}}{(x^{2} + y^{2})^{3}},\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= \frac{6 y^{2} - 2x^{2}}{(x^{2} + y^{2})^{3}} \;\;\;\;\;\text{e}\\ \frac{\partial^{2} f}{\partial y\partial x} &= \frac{8xy}{(x^{2} + y^{2})^{3}}.\end{aligned}$
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $z=\ln(1+x^{2}+y^{2})$.
$\begin{aligned}[t]\frac{\partial^{2} z}{\partial x^{2}} &= \frac{2 + 2y^{2} - 2x^{2}}{(1 + x^{2} + y^{2})^{2}},\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= \frac{2 + 2x^{2} - 2y^{2}}{(1 + x^{2} + y^{2})^{2}} \;\;\;\;\;\text{e}\\\frac{\partial^{2} z}{\partial x\partial y} &= \frac{\partial^{2} z}{\partial y\partial x}= \frac{-4xy}{(1 + x^{2} + y^{2})^{2}}.C\end{aligned}$
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função diferenciável de uma variável real e seja $f(x,y)=(x^{2}+y^{2})\phi \bigg(\dfrac{x}{y}\bigg).$
Mostre que
$$x\;\frac{\partial f}{\partial x}+y\;\frac{\partial f}{\partial y}=2f.$$
$\displaystyle \frac{\partial f}{\partial x} = 2x \phi \left( \frac{x}{y} \right) + \frac{(x^{2} + y^{2})}{y} \phi'\left( \frac{x}{y} \right)\ \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 2y \phi \left( \frac{x}{y} \right) - \frac{x(x^{2} + y^{2})}{y^{2}} \phi'\left( \frac{x}{y} \right).$
Verifique que a função $z=\ln(e^{x}+e^{y})$ é uma solução das equações diferenciais
$$\frac{\mathrm{\partial}z}{\mathrm{\partial}x} + \frac{\mathrm{\partial}z}{\mathrm{\partial}y}=1\;\;\;\;\;\;\; e\;\;\;\;\;\;\; \frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}^{2}x}+\frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}^{2}y}-\bigg(\frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}x\mathrm{\partial}y}\bigg)^{2}=0.$$
$\begin{aligned}[t]\frac{\partial z }{\partial x} &= \frac{e^{x}}{e^{x} + e^{y}},\;\;\; \frac{\partial z }{\partial y} = \frac{e^{y}}{e^{x} + e^{y}},\\\frac{\partial^{2} z }{\partial x^{2}} &= \frac{\partial^{2} z }{\partial y^{2}} = \frac{e^{x + y}}{(e^{x} + e^{y})^{2}},\;\;\; \frac{\partial^{2} z }{\partial x \partial y} = -\frac{e^{x + y}}{(e^{x} + e^{y})^{2}}.\end{aligned}$
Calcule as derivadas parciais de $f(x,y,z) = xe^{x - y - z}$.
$\displaystyle \frac{\partial f}{\partial x} = (1 + x)e^{x - y - z},\;\;\;\; \frac{\partial f}{\partial y} = -x e^{x - y - z}\;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial f}{\partial z} = -x e^{x - y - z}.$
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $f(x,y)=x^{3}y^{2}$.
$\displaystyle \frac{\partial^{2} f}{\partial x^{2}}= 2xy^{2},\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= 2x^{3}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} f}{\partial x\partial y}= \frac{\partial^{2} f}{\partial y\partial x}= 6x^{2}y.$
A função $p=p(V,T)$ é dada implicitamente pela equação $pV=nRT$, onde $n$ e $R$ são constantes não-nulas (Lei dos Gases Ideais). Calcule $\dfrac{\partial p}{\partial V}$ e $\dfrac{\partial p}{\partial T}.$
$\displaystyle \frac{\partial p}{\partial V} = -\frac{nRT}{V^{2}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial p}{\partial T} = \frac{nR}{V}.$
Determine as derivadas parciais de $f(x,y)=(4xy-3y^{3})^{3}+5x^{2}y$.
$\displaystyle \frac{\partial f}{\partial x} = 12 y (4xy - 3y^{3})^{2} + 10xy\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 3(4xy - 3y^{2})^{2}(4x - 9y^{2}) + 5x^{2}.$
Se $z=\sin(x+\sin{y})$, mostre que $\dfrac{\partial z}{\partial x} \;\dfrac{\partial^{2} z}{\partial x \partial y}=\dfrac{\partial z}{\partial y}\;\dfrac{\partial^{2}z}{\partial x^{2}}$.
$\begin{aligned}[t]\frac{\partial z}{\partial x} &= \cos(x + \sin y),\;\;\; \frac{\partial z}{\partial y} = \cos(x + \sin y) \cos y,\\\frac{\partial z^{2}}{\partial x\partial y} &= -\sin (x + \sin y) \cos y\;\;\text{e}\;\; \frac{\partial^{2} z}{\partial x^{2}} = -\sin (x + \sin y).\end{aligned}$
Determine as derivadas parciais de $z=\dfrac{x\sin{y}}{\cos(x^{2}+y^{2})}$.
$\begin{aligned}[t]\frac{\partial z}{\partial x} &= \frac{\sin y ( \cos(x^{2} + y^{2}) + 2x^{2} \sin(x^{2} + y^{2}))}{(\cos(x^{2} + y^{2}))^{2}}\;\;\;\;\;\;\text{e}\\\frac{\partial z}{\partial y} &= \frac{x \cos y \cos(x^{2} + y^{2}) + 2xy \sin y \sin(x^{2} + y^{2})}{(\cos(x^{2} + y^{2}))^{2}}.\end{aligned}$
Calcule as derivadas parciais de $w = x^2 \arcsin{\dfrac{y}{z}}$.
$\displaystyle \frac{\partial w}{\partial x} = 2x \arcsin \left( \frac{t}{z}\right),\;\;\;\; \frac{\partial w}{\partial y} = \frac{x^{2}|z|}{z\sqrt{z^{2} - y^{2}}} \;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial w}{\partial z} = - \frac{x^{2}y}{|z|\sqrt{z^{2} - y^{2}}}.$
Seja
$$f(x,y)=\begin{cases}\dfrac{x^{3}y-xy^{3}}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$$
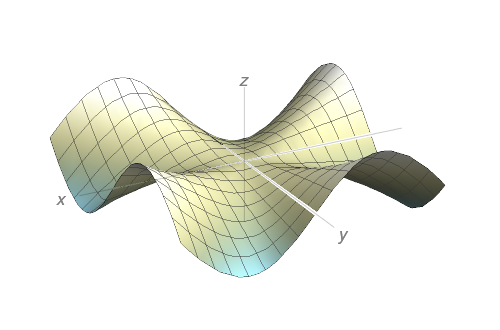
Use um computador para traçar o gráfico de $f$.
Determine $f_{x}(x,y)$ e $f_{y}(x,y)$ quando $(x,y)\neq (0,0).$
Determine $f_{x}(0,0)$ e $f_{y}(0,0)$ use a definição das derivadas parciais como limite.
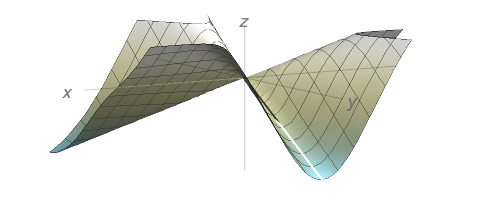
Mostre que $f_{xy}(0,0)=-1$ e $f_{yx}(0,0)=1$
O resultado da parte (d) contradiz o Teorema de Clairaut? Use o gráfico de $f_{xy}$ e $f_{yx}$ para ilustrar sua resposta.
- Gráfico de $f$:
- $\displaystyle f_{x} = \frac{x^{4}y + 4x^{2}y^{3} - y^{5}}{(x^{2} + y^{2})^{2}}\;\;\text{e}\;\;f_{y} = \frac{x^{5} - 4x^{3}y^{2} - xy^{4} }{(x^{2} + y^{2})^{2}}$ quando $(x,y)\neq (0,0).$
- $f_{x}(0,0) = f_{y}(0,0) = 0$.
- Use $\displaystyle f_{xy}(0,0)= \lim_{h \to 0} \frac{f_{x}(0,h) - f_{x}(0,0)}{h}\;\;\text{e}\;\;f_{yx}(0,0)= \lim_{h \to 0} \frac{f_{y}(h,0) - f_{y}(0,0)}{h}$.
- Para $(x,y) \neq (0,0),$ $\displaystyle f_{xy} = {x^{6} + 9x^{4}y^{2} - 9x^{2}y^{4} - y^{6}}{(x^{2} + y^{2})^{3}}.$ Como $f_{xy}$ não é contínua na origem, não há uma contradição com o Teorema de Clairaut. Os gráficos de $f_{xy}$ e $f_{yx}$ são idênticos, exceto na origem:
Verifique que $\dfrac{\partial ^{2}f}{\partial x^{2}}+\dfrac{\partial ^{2}f}{\partial y^{2}}=0$, onde $f(x,y)=\ln(x^{2}+y^{2}).$
$\displaystyle \frac{\partial^{2} f}{\partial x^{2}}= \frac{2 y^{2} - 2 x^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= \frac{2 x^{2} - 2 y^{2}}{(x^{2} + y^{2})^{2}}.$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=e^{-xyz}$.
$\displaystyle f_{x} = -yz e^{-xyz},\;\;\;\; f_{y} = -xz e^{-xyz}\;\;\;\;\text{e}\;\;\;\; f_{z} = -xy e^{-xyz}$.
Considere a função
$$f(x,y)= \begin{cases}\dfrac{xy^{2}}{x^{2}+y^{4}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$$
A função é contínua em $(0,0)$? Justifique sua resposta.
Determine as derivadas parciais $\dfrac{\partial f}{\partial x}(0,0)$ e $\dfrac{\partial f}{\partial y}(0,0)$.
Não, pois $\lim_{(x,y) \to (0,0)} f(x,y)$ não existe.
$\displaystyle \frac{\partial f}{\partial x}(0,0) = \frac{\partial f}{\partial y}(0,0) = 0$.
Seja $s = f(x,y,z,w)$ dada por $s = e^{\frac{x}{y} - \frac{z}{w}}$. Verifique que
$$x\dfrac{\partial s}{\partial x} + y \dfrac{\partial s}{\partial y} + z \dfrac{\partial s}{\partial z} + w \dfrac{\partial s}{\partial w} = 0.$$
$\begin{aligned}[t]\frac{\partial s}{\partial x} &= \frac{1}{y} e^{\frac{x}{y} - \frac{z}{w}},\;\;\;\;\;\frac{\partial s}{\partial y} = -\frac{x}{y^{2}} e^{\frac{x}{y} - \frac{z}{w}},\\\frac{\partial s}{\partial z} &= -\frac{1}{w} e^{\frac{x}{y} - \frac{z}{w}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial s}{\partial w} = \frac{z}{w^{2}} e^{\frac{x}{y} - \frac{z}{w}}.\end{aligned}$
Determine as derivadas parciais de $z=x^{2}\ln(1+x^{2}+y^{2})$.
$\displaystyle \frac{\partial z}{\partial x} = 2x\ln(1+ x^{2} + y^{2}) + \frac{2x^{3}}{1 + x^{2} + y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{2}y}{1 + x^{2} + y^{2}}.$
Determine as derivadas parciais de primeira ordem da função $f(x,y)=x^{5}+3x^{3}y^{2}+3xy^{4}$.
$\displaystyle \frac{\partial f}{\partial x} = 5x^{4} + 9x^{2}y^{2} + 3y^{4}\;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = 2x^{3}y + 12xy^{3}$.
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=x-\sqrt{y^{2}+z^{2}}$.
$\displaystyle f_{x} = 1,\;\;\;\; f_{y} = -\frac{y}{\sqrt{y^{2} + z^{2}}}\;\;\;\;\text{e}\;\;\;\; f_{z} = -\frac{z}{\sqrt{y^{2} + z^{2}}}$.
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=1/(x+y)$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{\partial f}{\partial y} = -\frac{1}{(x^{2} + y^{2})^{2}}$.
Verifique que $x\;\dfrac{\partial ^{2}z}{\partial x \partial y}+y\;\dfrac{\partial ^{2}z}{\partial y^{2}}=0$, onde $z=(x+y)e^{x/y}.$
$\displaystyle \frac{\partial^{2} z}{\partial x \partial y}= \frac{-3xy - x^{2}}{y^{3}}e^{\frac{x}{y}} \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= \frac{3x^{2}y + x^{3}}{y^{4}}e^{\frac{x}{y}}.$
$$x\;\dfrac{\partial z}{\partial x}+y\;\dfrac{\partial z}{\partial y}=z.$$
Primeiramente, vamos calcular $\dfrac{\partial z}{\partial x}$ e $\dfrac{\partial z}{\partial }.$ Assim,\\
$\bullet $ $\dfrac{\partial z}{\partial x}=$ $\dfrac{\partial}{\partial x}\bigg[x\cdot \sin\bigg(\dfrac{x}{y}\bigg)\bigg]=
1\cdot \sin\bigg(\dfrac{x}{y}\bigg)+x\cdot \cos \bigg(\dfrac{x}{y}\bigg)\cdot \dfrac{1}{y}$
$$=\sin\bigg(\frac{x}{y}\bigg)+\frac{x}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)$$
$\bullet $ $\dfrac{\partial z}{\partial y}=$ $\dfrac{\partial}{\partial y}\bigg[x\cdot \sin\bigg(\dfrac{x}{y}\bigg)\bigg]=
0\cdot \sin\bigg(\dfrac{x}{y}\bigg)+x\cdot \cos \bigg(\dfrac{x}{y}\bigg)\cdot \bigg(-\dfrac{x}{y^{2}}\bigg)$
$$=-\frac{x^{2}}{y^{2}}\cdot \cos\bigg(\frac{x}{y}\bigg).$$
Então,
$$x\cdot \frac{\partial z}{\partial x}+y\frac{\partial z}{\partial y}=x\cdot \bigg[\sin\bigg(\frac{x}{y}\bigg)+\frac{x}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)\bigg] +
y\cdot\bigg[ -\frac{x^{2}}{y^{2}}\cdot \cos\bigg(\frac{x}{y}\bigg)\bigg]$$
$$=x\cdot \sin\bigg(\frac{x}{y}\bigg)+\frac{x^{2}}{y}\cos\bigg(\frac{x}{y}\bigg)-\frac{x^{2}}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)$$
$$x\cdot \sin\bigg(\frac{x}{y}\bigg)=z.$$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=(x^{2}+y^{2}+z^{2})^{-1/2}$.
$\begin{aligned}[t]f_{x} &= -x(x^{2} + y^{2} + z^{2})^{-3/2},\;\; f_{y} = -y(x^{2} + y^{2} + z^{2})^{-3/2}\;\;\text{e}\\f_{z} &= -z(x^{2} + y^{2} + z^{2})^{-3/2}.\end{aligned}$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=e^{xy}\ln{y}$.
$\displaystyle \frac{\partial f}{\partial x} = ye^{xy}\ln y\;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = x e^{xy} \ln y + \frac{e^{xy}}{y}$.
A lei dos gases para uma massa fixa $m$ de um gás ideal à temperatura absoluta $T$, pressão $P$ e o volume $V$ é $PV=mRT$, onde $R$ é a constante do gás. Mostre que
$$\frac{\mathrm{\partial}P}{\mathrm{\partial}V}\frac{\mathrm{\partial}V}{\mathrm{\partial}T}\frac{\mathrm{\partial}T}{\mathrm{\partial}P}=-1.$$
$\displaystyle \frac{\partial P}{\partial V} = -\frac{mRT}{V^{2}},\;\;\;\frac{\partial V}{\partial T} = \frac{mR}{P}\;\;\;\text{e}\;\;\; \frac{\partial T}{\partial P} = \frac{V}{mR}.$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=e^{-(x^{2}+y^{2}+z^{2})}$.
$\displaystyle f_{x} = -2xe^{-(x^{2} + y^{2} + z^{2})},\;\;\;\; f_{y} = -2ye^{-(x^{2} + y^{2} + z^{2})}\;\;\;\;\text{e}\;\;\;\; f_{z} = -2ze^{-(x^{2} + y^{2} + z^{2})}$.
Seja $f(x,y)=\dfrac{x^{2}y^{2}}{x^{2}+y^{2}}.$
Calcule as derivadas parciais $\dfrac{\partial f}{\partial x}(x,y)$ e $\dfrac{\partial f}{\partial y}(x,y)$, num ponto $(x,y)\neq\;(0,0).$
Calcule o limite, se existir.
$$\lim_{(x,y)\rightarrow (0,0)}\frac{\partial f}{\partial x}(x,y)$$
$\displaystyle \frac{\partial f}{\partial x} = \frac{2xy^{4}}{(x^{2} + y^{2})^{2}} \;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = \frac{2x^{4}y}{(x^{2} + y^{2})^{2}}$.
$\displaystyle \lim_{(x,y)\rightarrow (0,0)}\frac{\partial f}{\partial x}(x,y) = 0$.
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=\ln(x+2y+3z)$.
$\displaystyle f_{x} = \frac{1}{x + 2y + 3z},\;\;\;\; f_{y} = \frac{2}{x + 2y + 3z}\;\;\;\;\text{e}\;\;\;\; f_{z} = \frac{3}{x + 2y + 3z}$.
Determine as derivadas parciais de primeira ordem da função $u=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdot \cdot \cdot +x_{n}^{2}}$.
$\displaystyle \frac{\partial u}{\partial x_{i}}= \frac{x_{i}}{\sqrt{x_{1}^{2}+x_{2}^{2}+\cdot \cdot \cdot +x_{n}^{2}}}$ para todo $i = 1, \cdots, n$.
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=(x^{2}-1)(y+2)$.
$\displaystyle \frac{\partial f}{\partial x} = 2x(y + 2) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = x^{2} - 1$.
A temperatura $T$ de uma localidade do Hemisfério Norte depende da longitude $x$, da latitude $y$ e do tempo $t$, de modo que podemos escrever $T=f(x,y,t)$. Vamos medir o tempo em horas a partir do início de Janeiro.
Qual é o significado das derivadas parciais $\partial T/\partial x$, $\partial T/\partial y$ e $\partial T/\partial t$?
Honolulu (você sabe onde fica?) tem longitude de $158^{\circ}W$ e latitude de $21^{\circ}N$. Suponha que às 9 horas em $1^{\circ}$ de Janeiro esteja ventando para nordeste uma brisa quente, de forma que a oeste e a sul o ar esteja quente e a norte e leste o ar esteja mais frio. Você esperaria que $f_{x}(158,21,9)$, $f_{y}(158,21,9)$ e $f_{t}(128,21,9)$ fossem positivas ou negativas? Explique.
- $\partial T/\partial x$ é a taxa de variação da temperatura quando a longitude muda, mas a latitude e o tempo são constantes;
$\partial T/\partial y$ é a taxa de variação da temperatura quando a latitude muda, mas a longitude e o tempo são constantes;
$\partial T/\partial t$ é a taxa de variação da temperatura quando o tempo muda, mas a longitude e a latitude são constantes. - $f_{x}(158,21,9) > 0,$ $f_{y}(158,21,9) < 0$ e $f_{t}(158,21,9) > 0.$
Determine as derivadas parciais de $f(x,y)=e^{-x^{2}-y^{2}}$.
$\displaystyle \frac{\partial f}{\partial x} = -2xe^{-x^{2} - y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = -2ye^{-x^{2} - y^{2}}.$
Seja $w=f(x,y,z)$ uma função de três variáveis independentes. Escreva a definição formal de derivada parcial $\partial f/\partial z$ em $(x_{0},y_{0},z_{0})$. Use essa definição para encontrar $\partial f/\partial z$ em $(1,2,3)$ para $f(x,y,z)=x^{2}yz^{2}.$
$\displaystyle \frac{\partial f}{\partial z}(1,2,3) = 12$.
Seja $f(x,y,z) = \dfrac{x}{x^2 + y^2 + z^2}$.
Verifique que
$$x\dfrac{\partial f}{\partial x} + y\dfrac{\partial f}{\partial y} + z\dfrac{\partial f}{\partial z} = -f.$$
$\displaystyle \frac{\partial f}{\partial x} = \frac{-x^{2} + y^{2} + z^{2}}{(x^{2} + y^{2} + z^{2})^{2}},\;\;\;\; \frac{\partial f}{\partial y} = \frac{-2xy}{(x^{2} + y^{2} + z^{2})^{2}} \;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial f}{\partial z} = \frac{-2xz}{(x^{2} + y^{2} + z^{2})^{2}}.$
Determine as derivadas parciais de $z=xye^{xy}$.
$\displaystyle \frac{\partial z}{\partial x} = ye^{xy} (1 + xy) \;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = xe^{xy} (1 + xy).$
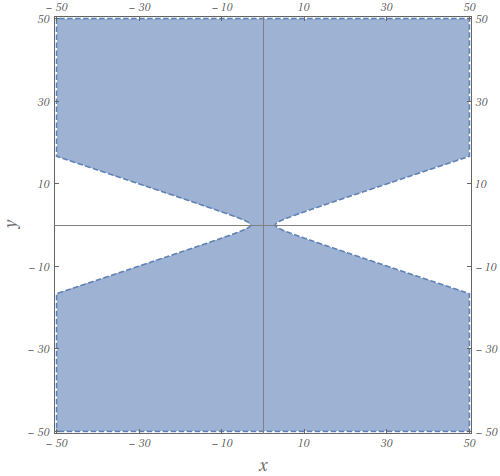
Considere a função
$$f(x,y)=\log(9-x^{2}-9y^{2}).$$
Esboce no plano $xy$ o domínio de $f.$
Calcule as derivadas parciais $f_{x}$ e $f_{y}.$
- $D_{f} = \left\lbrace (x,y) \in \mathbb{R}^{2};\; x^{2} -9y^{2} < 9 \right\rbrace$.
- $\displaystyle f_{x} = \frac{-2x}{9 - x^{2} - 9y^{2}} \;\;\;\text{e}\;\;\;f_{y} = \frac{-18y}{9 - x^{2} - 9y^{2}}$.

