Gradiente
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Determine um plano que seja tangente à superfície $x^2 + 3y^2 + 2z^2 = \dfrac{11}{6}$ e paralelo ao plano $x + y + z = 10$.
$\displaystyle x + y + z = \frac{11}{6}$ ou $\displaystyle x + y + z = -\frac{11}{6}.$
Determine os pontos da superfície $x^2 + 2y^2 + 3z^2 = 1$ nos quais o plano tangente é paralelo ao plano $3x - y + 3z = 1$.
$\displaystyle \left(\frac{3\sqrt{2}}{5}, - \frac{1}{5\sqrt{2}}, \frac{\sqrt{2}}{5} \right)$ e $\displaystyle \left(-\frac{3\sqrt{2}}{5}, \frac{1}{5\sqrt{2}}, -\frac{\sqrt{2}}{5} \right).$
Existem pontos no hiperboloide $x^2 - y^2 - z^2 = 1$ nos quais o plano tangente é paralelo ao plano $z = x + y$?
Não.
No item abaixo :
- determine o gradiente de $f$;
- calcule o gradiente no ponto $P$; e
- determine a taxa de variação de $f$ em $P$ na direção do vetor $\bf{u}$.
$f(x,y,z) = \sqrt{x+yz}, P = (1,3,1), \bf{u} = \left( \frac{2}{7}, \frac{3}{7}, \frac{6}{7} \right)$.
- $\displaystyle \nabla f(x,y,z) = \left(\frac{1}{2\sqrt{x + yz}}, \frac{z}{2\sqrt{x + yz}}, \frac{y}{2\sqrt{x + yz}} \right).$
- $\displaystyle \nabla f(1,3,1) = \left(\frac{1}{4}, \frac{1}{4}, \frac{3}{4}\right).$
- $\displaystyle \frac{23}{28}.$
Seja $f$ uma função de duas variáveis que tenha derivadas parciais contínuas e considere os pontos $A = (1,3)$, $B = (3,3)$, $C = (1,7)$ e $D = (6,15)$. A derivada direcional em $A$ na direção do vetor $\overrightarrow{AB}$ é 3, e a derivada direcional em $A$ na direção $\overrightarrow{AC}$ é 26. Determine a derivada direcional de $f$ em $A$ na direção do vetor $\overrightarrow{AD}$.
$\displaystyle \frac{327}{13}.$
A temperatura $T$ em uma bola de metal é inversamente proporcional à distância do centro da bola, que tomamos como a origem. A temperatura no ponto $(1,2,2)$ é de 120°.
- Determine a taxa de variação de $T$ em $(1,2,2)$ em direção ao ponto $(2,1,3)$.
- Mostre que em qualquer ponto da bola a direção de maior crescimento na temperatura é dada por um vetor que aponta para a origem.
- $\displaystyle -\frac{40}{3\sqrt{3}}.$
- Note que $\nabla T = -360 (x^{2} + y^{2} + z^{2})^{-3/2} (x,y,z)$ sempre aponta para a origem.
Defina gradiente de uma função de três variáveis. Calcule $\nabla f(x,y,z)$.
$f(x,y,z) = x^2 + y^2 + z^2$
$\displaystyle \nabla f(x,y,z) = (2x,2y,2z).$
No item abaixo :
- determine o gradiente de $f$;
- calcule o gradiente no ponto $P$; e
- determine a taxa de variação de $f$ em $P$ na direção do vetor $\bf{u}$.
$f(x,y,z) = xe^{2yz}, P = (1,-3), \bf{u} = \left( \frac{2}{3}, -\frac{2}{3}, \frac{1}{3} \right)$.
- $\nabla f(x,y,z) = (e^{yz}, 2xze^{2yz}, 2xye^{2yz}).$
- $\nabla f(3,0,2) = (1,12,0).$
- $\displaystyle -\frac{22}{3}.$
Mostre que uma função diferenciável $f$ decresce mais rapidamente em $\bf{x}$ na direção oposta à do vetor gradiente, ou seja, na direção de $-\nabla f(\bf{x})$.
Se $\bf{u}$ é um versor e $\theta$ é o ângulo entre $\nabla f$ e $\bf{u},$ então
$$
D_{\bf{u} f} = \nabla f \cdot \bf{u} = |\nabla f||\bf u| \cos(\theta) = |\nabla f|\cos(\theta).
$$
O valor mínimo de $\cos(\theta)$ é $-1$ e isto ocorre quando $\theta = \pi.$ Portanto o valor mínimo de $D_{\bf{u}} f$ é $-|\nabla f|$ e ocorre quando $\theta = \pi,$ ou seja, quando $\bf{u}$ tem a direção oposta à de $\nabla f.$
Seja $f(x,y) = x \arctan{\dfrac{x}{y}}$. Calcule $D_{\bf{u}}f(1,1)$, em que $\bf{u}$ aponta na direção e sentido de máximo crescimento de $f$, no ponto $(1,1)$.
$\displaystyle D_{\bf{u}}f(1,1) = \sqrt{\left( \frac{\pi}{4} + \frac{1}{2}\right)^{2} + \frac{1}{4}}.$
Determine a equação da reta tangente à curva de nível dada, no ponto dado.
$e^{2x - y} + 2x + 2y = 4$, em $\left(\dfrac{1}{2},1\right)$.
$y = -4x + 3.$
Mostre que a equação do plano tangente ao elipsoide $x^2/a^2 + y^2/b^2 + z^2/c^2 = 1$ no ponto $(x_0,y_0,z_0)$ pode ser escrita como
$$\dfrac{xx_0}{a^2} + \dfrac{yy_0}{b^2} + \dfrac{zz_0}{c^2} = 1.$$
Note que se $F(x,y,z) = x^2/a^2 + y^2/b^2 + z^2/c^2 - 1,$ então
$$
\nabla F(x_{0},y_{0},z_{0}) = 2 \left(\frac{x_{0}}{a^{2}},\frac{y_{0}}{b^{2}},\frac{z_{0}}{c^{2}} \right)
$$
e a equação do plano tangente em $(x_{0},y_{0},z_{0})$ é
$$
\nabla F(x_{0},y_{0},z_{0}) \cdot (x,y,z) = \nabla F(x_{0},y_{0},z_{0}) \cdot (x_{0},y_{0},z_{0}) = 2.
$$
A temperatura em um ponto $(x,y,z)$ é dada por
$$T(x,y,z) = 200e^{-x^2 - 3y^2 - 9z^2},$$
em que $T$ é medido em °C e $x,y$ e $z$ em metros.
- Determine a taxa de variação da temperatura no ponto $P = (2,-1,2)$ em direção ao ponto $(3,-3,3)$.
- Qual é a direção de maior crescimento da temperatura em $P$?
- Encontre a taxa máxima de crescimento em $P$.
- $\displaystyle \frac{5200\sqrt{6}}{3e^{43}}$ ºC/m.
- $400 e^{-43} (-2,3,-18).$
- $400 e^{-43}\sqrt{337}$ ºC/m.
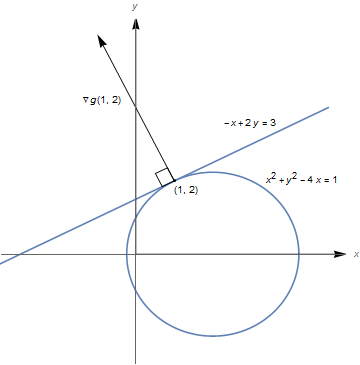
Se $g(x,y) = x^2 + y^2 - 4x$, encontre o vetor gradiente $\nabla g(1,2)$ e use-o para encontrar a reta tangente à curva de nível $g(x,y) = 1$ no ponto $(1,2)$. Esboce a curva de nível, a reta tangente e o vetor gradiente.
$\nabla g(1,2) = (1,2) = (-2,4);$ reta tangente à curva de nível $g(x,y) = 1$ em $(1,2)$: $-x + 2y = 3.$
Em que direção e sentido a função dada cresce mais rapidamente no ponto dado? E em que direção e sentido decresce mais rapidamente?
$f(x,y) = \ln{||(x,y)||}$ em $(1,-1)$.
Cresce: $(1,-1)$; descresce: $(-1,1).$
Suponha que em uma certa região do espaço o potencial elétrico $V$ seja dado por $V(x,y,z) = 5x^2 - 3xy + xyz.$
- Determine a taxa de variação do potencial em $P = (3,4,5)$ na direção do vetor $\bf{v} = \bf{i} + \bf{j} - \bf{k}$.
- Em que direção $V$ varia mais rapidamente em $P$?
- Qual a taxa máxima de variação em $P$?
- Queremos determinar o valor de $D_\bf{u}f(P)$, em que $\bf{u}$ é o vetor unitário que tem mesma direção de $\bf{v}$, isto é, $\bf{u} = \frac{1}{\sqrt{3}}(1,1,-1)$. Como $V$ é diferenciável, segue que $D_\bf{u}f(P) = \nabla V(P) \cdot \mathbf{u}$. Observe que \linebreak $\nabla V(x,y,z) = (10x-3y+yz,-3x+xz,xy)$. Logo $\nabla V(P) = (38,6,12)$. Portanto, $$D_\bf{u}f(P) = \nabla V(P) \, \cdot \, \mathbf{u} = (38,6,12) \, \cdot \, \dfrac{1}{\sqrt{3}}(1,1,-1) = \dfrac{32\sqrt{3}}{3}.$$
- A direção em que $V$ varia mais rapidamente no ponto $P$ é a direção do gradiente de $V$ no ponto $P$, isto é, na direção de $\nabla V(P) = (38,6,12)$. Observe que aqui não é necessário normalizar o vetor, pois o exercício pede apenas a direção.
- A taxa de variação máxima é $|\nabla V(P)| = 2\sqrt{406}$.
Determine a taxa de variação máxima de $f$ no ponto dado e a direção em que isso ocorre.
$f(x,y) = \dfrac{y^2}{x}, (2,4).$
$4\sqrt{2}.$
Em que direção e sentido a função dada cresce mais rapidamente no ponto dado? E em que direção e sentido decresce mais rapidamente?
$f(x,y) = \sqrt{4 - x^2 - 2y^2}$ em $\left(1,\dfrac{1}{2}\right)$.
Cresce: $(-1,-1)$; descresce: $(1,1).$
Calcule $\nabla f(x,y)$.
$f(x,y) = \dfrac{x}{y}$
$\displaystyle \nabla f(x,y) = \left(\frac{1}{y}, -\frac{x}{y^{2}} \right).$
Determine a equação da reta tangente à curva de nível dada, no ponto dado.
$x^2 + xy + y^2 - 3y = 1$, em $(1,2)$.
$y - 2 = -2(x - 1).$
Calcule $\nabla f(x,y)$.
$f(x,y) = \arctan{\dfrac{x}{y}}$
$\displaystyle \nabla f(x,y) = \left(\frac{y }{x^{2} + y^{2}}, -\frac{x}{x^{2} + y^{2}} \right).$
Defina gradiente de uma função de três variáveis. Calcule $\nabla f(x,y,z)$.
$f(x,y,z) = \sqrt{x^2 + y^2 + z^2}$
$\displaystyle \nabla f(x,y,z) = \frac{1}{\sqrt{x^{2} + y^{2} + z^{2}}}.$
Determine todos os pontos nos quais a direção de maior variação da função $f(x,y) = x^2 + y^2 - 2x - 4y$ é $\bf{i} + \bf{j}$.
$\left\lbrace (x,y) \in \mathbb{R}^{2}; y =x + 1 \right\rbrace.$
Defina gradiente de uma função de três variáveis. Calcule $\nabla f(x,y,z)$.
$f(x,y,z) = z \arctan{\dfrac{x}{y}}$
$\displaystyle \nabla f(x,y,z) = \left(\frac{yz}{x^{2} + y^{2}},-\frac{xz}{x^{2} + y^{2}},\arctan\left(\frac{x}{y}\right) \right).$
Determine a taxa de variação máxima de $f$ no ponto dado e a direção em que isso ocorre.
$f(x,y,z) = \sqrt{x^2 + y^2 + z^2}, (3,6,-2).$
$1.$
$f(x,y) = \sin{xy}, (1,0).$
$1.$
A temperatura em um ponto $(x,y)$ é $T(x,y)$, medida em graus Celsius. Um inseto rasteja de modo que sua posição depois de
$t$ segundos seja dada por $x=\sqrt{1+t}$ e $y=2+\dfrac{1}{3}t$, onde $x$ e $y$ são medidas em centímetros. A função temperatura satisfaz
$T_{x}(2,3)=4$ e $T_{y}(2,3)=3$. Quão rápido a temperatura aumenta no caminho do inseto depois de três segundos?
A temperatura aumenta a uma taxa de $2º$C/s.
Mostre que a operação de calcular o gradiente de uma função tem a propriedade fornecida. Suponha que $u$ e $v$ sejam funções de $x$ e $y$, diferenciáveis, e $a$ e $b$ sejam constantes.
$\nabla (au + bv) = a \nabla u + b \nabla v$
$\nabla\left(\dfrac{u}{v}\right) = \dfrac{v \nabla u - u \nabla v}{v^2}$
$\nabla(uv) = u \nabla v + v \nabla u$
$\nabla u^n = nu^{n-1}\nabla u$
Pelas propriedades análogas para derivadas parciais e a linearidade de vetores, os quatro itens são válidos.
No item abaixo :
- determine o gradiente de $f$;
- calcule o gradiente no ponto $P$; e
- determine a taxa de variação de $f$ em $P$ na direção do vetor $\bf{u}$.
$f(x,y) = y \ln{x}, P = (1, -3), \bf{u} = \left(-\frac{4}{5}, \frac{3}{5} \right)$.
- $\nabla f(x,y) = (y/x,\ln(x)).$
- $\nabla f(1,-3) = (-3,0).$
- $\displaystyle \frac{12}{5}.$
Determine a taxa de variação máxima de $f$ no ponto dado e a direção em que isso ocorre.
$f(x,y,z) = \dfrac{x + y}{z}, (1,1,-1).$
$\sqrt{6}.$
No item abaixo :
- determine o gradiente de $f$;
- calcule o gradiente no ponto $P$; e
- determine a taxa de variação de $f$ em $P$ na direção do vetor $\bf{u}$.
$f(x,y) = 5xy^2 - 4x^3y, P = (1,2), \bf{u} = \left( \frac{5}{13},\frac{12}{13} \right)$.
- $\nabla f(x,y) = (5y^{2} - 12x^{2}y, 10xy - 4x^{3}).$
- $\nabla f(1,2) = (-4, 16).$
- $\displaystyle \frac{172}{13}.$
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado.
$x^2 + 3y^2 + 4z^2 = 8$, em $(1,-1,1)$.
Plano tangente: $x - 3y + 4z = 8$
Reta normal: $(x,y,z) = (1,-1,1) + \lambda (2,-6,8),$ $\lambda \in \mathbb{R}.$
Calcule $\nabla f(x,y)$.
$f(x,y) = x^2y$
$\displaystyle \nabla f(x,y) = (2xy,x^{2}).$
Considere a função
$$f(x,y) = \ln{(x^2 + y^2)}.$$
- Determine a taxa de variação máxima de $f$ em $(1,1)$ e a direção em que isso ocorre.
- Determine a derivada direcional de $f$ em $(1,1)$ na direção do vetor $\bf{v} = (3,4)$.
- Na direção do vetor $(1,1).$ O valor da taxa máxima é $\sqrt{2}.$
- $ \displaystyle \frac{7}{5}.$
Determine uma reta que seja tangente à curva $x^2 + xy + y^2 = 7$ e paralela à reta $4x + 5y = 17$.
$\displaystyle y - 2 = -\frac{4}{5} (x - 1)$ ou $\displaystyle y + 2 = -\frac{4}{5} (x + 1).$
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado.
$x^2 - 2y^2 + z^2 + yz = 2$ em $(2,1,-1).$
Plano tangente: $4x - 5y - z = 4$,
Reta normal: $(x,y,z) = (2,1,-1) + \lambda (4,-5,-1),$ $\lambda \in \mathbb{R}.$
Determine a taxa de variação máxima de $f$ no ponto dado e a direção em que isso ocorre.
$f(x,y,z) = \tan{(x + 2y + 3z)}, (-5,1,1).$
$\sqrt{14}.$
- Duas superfícies são ditas \textbf{ortogonais} em um ponto de intersecção se suas normais são perpendiculares nesse ponto. Mostre que superfícies com equação $F(x,y,z) = 0$ e $G(x,y,z) = 0$ são ortogonais em um ponto $P$, em que $\nabla F \neq 0$ e $\nabla G \neq 0$, se, e somente se, em $P$, $$F_xG_x + F_yG_y + F_zG_z = 0.$$
- Use a parte 1. para mostrar que as superfícies $z^2 = x^2 + y^2$ e $x^2 + y^2 + z^2 = r^2$ são ortogonais em todo ponto de intersecção. Você pode ver isso sem fazer os cálculos?
- Note que a direção da normal de $F$ é dada por $\nabla F,$ a de $G$ por $\nabla G$ e que duas normais em $P$ são perpendiculares se $\nabla F \cdot \nabla G = 0.$
- Tome $F = x^2 + y^2 - z^2,$ $G = x^2 + y^2 + z^2 - r^2$ e verifique $(a).$ Para "ver" isso sem calcular, note que $F = 0$ é a equação de um cone circular com vértice na origem e $G = 0$ é a equação de uma esfera centrada na origem.
Seja $g(x,y) = f(x^2 + y^2)$, em que $f$ é uma função diferenciável. Sabendo que $f'(2) = 1$, determine a equação da reta tangente à curva de nível de $g$ que passa pelo ponto $(1,1)$.
$x + y = 2.$
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado.
$2xyz = 3$, em $\left(\dfrac{1}{2},1,3\right)$.
Plano tangente: $6x + 3y + z = 9$,
Reta normal: $(x,y,z) = \left(\frac{1}{2},1,3\right) + \lambda (6,3,1),$ $\lambda \in \mathbb{R}.$
Considere o vetor unitário $\bf{u} = (\sqrt{3}/2,1/2)$ e a função
$$f(x,y) = \begin{cases}
\dfrac{xy^2}{x^2 + y^4}, & \text{se } (x,y) \neq (0,0),\\ 0, & \text{se } (x,y) = (0,0).\end{cases}$$
- Determine a derivada direcional $D_{\bf{u}}f(0,0)$.
- Explique por que o produto escalar $\nabla f(0,0) \cdot \bf{u}$ não fornece a derivada direcional de $f$ em $(0,0)$ na direção de $\bf{u}$.
- $\displaystyle \frac{\sqrt{3}}{6}.$
- Pois $f$ não é diferenciável em $(0,0),$ já que não é contínua nesse ponto.
Em que direção e sentido a função dada cresce mais rapidamente no ponto dado? E em que direção e sentido decresce mais rapidamente?
$f(x,y) = x^2 + xy + y^2$ em $(1,1)$.
Cresce: $(3,3)$; descresce: $(-3,-3).$
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado.
$ze^{x - y} + z^3 = 2$ em $(2,2,1)$.
Plano tangente: $x - y + 4z = 4$,
Reta normal: $(x,y,z) = (2,2,1) + \lambda (1,-1,4),$ $\lambda \in \mathbb{R}.$
Seja
$$f(x,y) = x - y\sin{(\pi(x^2 + y^2))}.$$
- Calcule a derivada direcional de $f$ no ponto $(0,0)$ na direção de $\bf{v} = (1/2,\sqrt{3}/2)$.
- Em que direção a taxa de variação de $f$ no ponto $(0,0)$ é máxima? Qual é o valor da taxa máxima nesse ponto?
- $ \displaystyle \frac{1}{2}.$
- Na direção do vetor $(1,0).$ O valor da taxa máxima é $1.$
A superfície de um lago é representada por uma região $D$ no plano $xy$, tal que a profundidade (em pés) sob o ponto correspondente a $(x,y)$ é dada por
$$f(x,y) = 300 - 2x^2 - 3y^2.$$
Se um nadador está no ponto $(4,9)$, em que direção deve nadar para que a profundidade sob ele decresça mais rapidamente?
Na direção dada pelo vetor $(16,54).$
Determine uma reta que seja tangente à elipse $2x^2 + y^2 = 3$ e paralela à reta $2x + y = 5$.
$\displaystyle y = -2x + 3$ ou$\displaystyle y = -2x - 3.$
Calcule $\nabla f(x,y)$.
$f(x,y) = e^{x^2 - y^2}$
$\displaystyle \nabla f(x,y) = e^{x^{2} - y^{2}}(2x,-2y).$
Defina gradiente de uma função de três variáveis. Calcule $\nabla f(x,y,z)$.
$f(x,y,z) = (x^2 + y^2 + 1)^{z^2}$
$\displaystyle \nabla f(x,y,z) = (x^{2} + y^{2} + 1)^{z^{2}-1}\left(2xz^{2},2yz^{2},2z(x^{2} + y^{2} + 1)\ln(x^{2} + y^{2} + 1)\right).$
Determine as equações paramétricas da reta tangente à curva formada pela intersecção do paraboloide $z = x^2 + y^2$ com o elipsoide $4x^2 + y^2 + z^2 = 9$ no ponto $(-1,1,2)$.
$(x,y,z) = (-1,1,2) + \lambda (-10, -16, -12),$ $\lambda \in \mathbb{R}.$

