Vetores
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Mostre que: se um triângulo tem duas medianas iguais então ele é isósceles.
Seja o triângulo $\ ABC$, $M$ o ponto médio de $\overrightarrow{BN}$ e $N$ o de $\overrightarrow{AC}.$ Seja também $P$ a interseção de $\overrightarrow{BN}$ e $\overrightarrow{AM},$ e por hipótese, temos $\left\Vert \overrightarrow{BN}\right\Vert =\left\Vert\overrightarrow{AM}
\right\Vert .$ Observe que os triângulos $NPM$ e $APB$ são isósceles. Observe também que como $\overrightarrow{MN}$ é paralelo a $\overrightarrow{AB}$ os ângulos $N\widehat{P}A$ e $M\widehat{P}B$ são iguais. Assim, pela lei dos cossenos, temos
$\left\Vert \overrightarrow{AN}\right\Vert ^{2}=\left\Vert \overrightarrow{PN}-\overrightarrow{PA}\right\Vert ^{2}=\left\Vert \overrightarrow{PM}-\overrightarrow{PB}\right\Vert ^{2}=\left\Vert \overrightarrow{BM}\right\Vert ^{2}$
Como, $2\left\Vert \overrightarrow{AN}\right\Vert =\left\Vert \overrightarrow{AC}\right\Vert $e $2\left\Vert \overrightarrow{BM}\right\Vert =\left\Vert \overrightarrow{BC}\right\Vert ,$ então $\left\Vert \overrightarrow{AN}\right\Vert =\left\Vert \overrightarrow{BC}\right\Vert ,$ e portanto, o triângulo é isósceles.
Mostre que o segmento que une os pontos médios de 2 lados de um triângulo é paralelo ao terceiro lado e é igual a sua metade.
Considere o triângulo $ABC,$ sendo $M$ o ponto médio do lado $AC$ e $N$ o do lado $BC.$ Assim, podemos escrever $\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\frac{1}{2} \overrightarrow{AC}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2} \overrightarrow{AB}.$
Portanto, concluímos que $MN//AB$ e $\left\Vert \overrightarrow{MN}\right\Vert =\left\Vert \overrightarrow{AB}\right\Vert .$
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
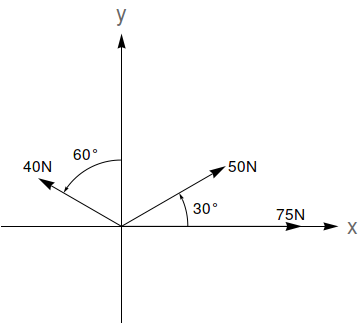
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
Verifique se os seguintes pontos são colineares: $A=(0,1,-1)$, $B=(1,2,0)$ e $C=(0,2,1)$.
Os pontos não são colineares.
Dados dois vetores $\vec{A}$ e $\vec{B}$, e $\theta$ o ângulo entre eles, ache fórmulas para $\|\vec{A} + \vec{B}\|$ e $\|\vec{A} - \vec{B}\|$ (Sugestão: use a Lei dos Cossenos).
$\|\vec{A} + \vec{B}\|^2=\|\vec{A}\|^2+\|\vec{B}\|^2 +2\|\vec{A}\|\|\vec{B}\|\cos\theta$.
Sejam $\vec{u}=(2,1,3)$, $\vec{v}=(0,1,-1)$ e $\vec{w}=(4,5,3)$ vetores do espaço.
Calcule $\vec{u}+\vec{v} $ e $\vec{u}-2\vec{v}+3\vec{w}$.
Determine $a$ e $b$ tais que $\vec{w}=a\vec{u}+b\vec{v}$.
- $\vec{u}+\vec{v}=(2,1,2) $ e $\vec{u}-2\vec{v}+3\vec{w}=(14,14,14)$.
- $a=2$ e $b=3$.
Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(1,-2,1)$ e sua origem é o ponto $P=(1,0,1)$.
$(2,-2,2)$.
Dados $A=(4,8,11)$, $B=(-3,1,4)$ e $C=(2,3,-3)$, faça uma figura esquemática, verificando que os pontos formam um triângulo, e:
Ache os tamanhos dos três lados do triângulo.
Ache os pontos médios dos três lados.
Calcule a soma dos vetores $\vec{AB}$, $\vec{BC}$ e $\vec{CA}$. Por que a soma é nula?
Ache o ponto em $AB$ cuja coordenada $y$ é $5$.
Ache os três pontos nos planos coordenados em $AB$ (extendidos).
Ache o ângulo entre $\vec{AB}$ e $\vec{BC}$ (sugestão: use a Lei dos Cossenos).
Ache os dois pontos de trisecção em $BC$ (internamente).
Ache o tamanho da altura saindo de $B$ e oposta ao lado $AC$.
Calcule a área do triângulo $ABC$.
Ache o tamanho da reta que bissecta o ângulo em $C$ (sugestão: use $\cos \theta/2 = \sqrt{(1+\cos\theta)/2}$; use trigonometria de triângulos retângulos).
Ache o raio e o centro do círculo circunscrito ao triângulo (sugestão: a hipotenusa é o diâmetro).
Ache os três pontos $D$ tais que $ABCD$ é um paralelogramo.
Para dois vetores $\vec{A}$ e $\vec{B}$, mostre que vale a Lei Distributiva: $m(\vec{A} + \vec{B})=m\vec{A}+m\vec{B}$ (Sugestão: mostre que $m\vec{A}+m\vec{B}$ está na mesma direção que $\vec{A}+\vec{B}$ e que $\|m\vec{A}+m\vec{B}\|$ é igual a $m$ vezes $\|\vec{A}+\vec{B}\|$). O que ocorre se $m$ for negativo?
Sejam $\vec{OA}$ e $\vec{OB}$ dois vetores não colineares no espaço. Qual o conjunto dos pontos $P$ tais que $\vec{OP} = \lambda\vec{OA}+(1-\lambda)\vec{OB}$?
Trata-se da reta passando pelos pontos $A$ e $B$.
Quais são os cossenos diretores do vetor de $(2,-3,5)$ a $(-1,1,-7$)?
$-3/13,4/13,-12/13$.
Verifique se os seguintes pontos são colineares: $A=(1,0,1)$, $B=(2,2,0)$ e $C=(0,-2,2)$.
Os pontos são colineares.
Considere três vetores do $\mathbb{R}^{3}$: $u = (1,0,-1)$, $v = (1,1,1)$ e $w = (x,y,z)$.
Se $w = (-1,-5,-9)$, mostre que existem escalares $a$ e $b$ tais que $w = au + bv$.
Ainda para $w = (-1,-5,-9)$, existem escalares $a', b'$ tais que $(a',b') \ne (a,b)$ e $w = a'u + b'v$?
Para todo $w$ existem escalares $a$ e $b$ tais que $w = au + bv$ como no item anterior?
Existe alguma relação entre as perguntas acima e o estudo de sistemas?
- $a=4$ e $b=-5$.
- Não.
- Não. Com apenas dois vetores não é possível gerar todos os vetores de $\mathbb{R}^3$. Por exemplo, não existem $\alpha$ e $\beta\in\mathbb{R}$ tais que $\alpha u + \beta v=(-1,5,9)$.
- Uma conclusão básica é que nem todo sistema de três equações e duas incógnitas terá solução. Mais conclusões são possíveis.
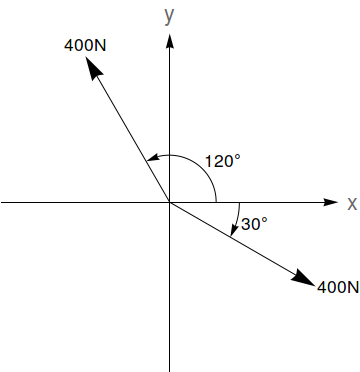
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
Dados os pontos $A=(1,0,1)$, $B=(-1,1,1)$ e $C=(0,1,2)$.
Determine o ponto $D$ tal que $A$, $B$, $C$ e $D$ sejam os vértices consecutivos de um paralelogramo.
Determine o ponto médio entre $A$ e $C$ e o ponto médio entre $B$ e $D$.
- \( D=(2,0,2)\)
- \(\dfrac{1}{2}(A+C)=(\dfrac{1}{2},\dfrac{1}{2},\dfrac{3}{2})=\dfrac{1}{2}(B+D)\)
Quais são os cossenos diretores da reta que passa pela origem no primeiro octante e que tem ângulos iguais com os três eixos coordenados?
$1/\sqrt{3},1/\sqrt{3},1/\sqrt{3}$.
Verifique se os seguintes pontos são colineares: $A=(3,1,4)$, $B=(2,7,1)$ e $C=(0,1,5)$.
Os pontos não são colineares.
Mostre que as diagonais de um paralelogramo se cortam ao meio (Sugestão: Sejam $M$ e $N$ os pontos médios das duas diagonais. Mostre que $\overline{MN}=\vec{0}$.).
Considere o paralelogramo $ABCD$, de diagonais $AC$ e $DB.$ Seja $M$ o ponto médio de $AC.$ Vamos provar que $M$ é também ponto médio de $BD.$ Ora, $\overrightarrow{BM}=\overrightarrow{BC}+ \overrightarrow{CM}=\overrightarrow{AD}+\overrightarrow{MA}=\overrightarrow{MD}.$ Logo, $M$ é o ponto médio de $BD.$
Um ponto $(x,y,z)$ se move tal que sua distância ao ponto $(3,2,4)$ é sempre $5$. Qual figura $(x,y,z)$ traça? Faça um esboço de uma parte dessa figura (um octante). Escreva uma equação simplificada que os pontos $(x,y,z)$ devem satisfazer.
Uma esfera com centro $(3,2,4)$, raio $5$, com equação $x^2+y^2+z^2-6x-4y-8z+4=0$.
Mostre que as medianas de um triângulo interceptam-se em um único ponto. Encontre a razão em que esse ponto divide cada mediana.
Tente generalizar o item (a) para tetraedros.
$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM},$ $\overrightarrow{BH}=\frac{2}{3}\overrightarrow{BN},$ $\overrightarrow{CI}=\frac{2}{3}\overrightarrow{CP}.$
Assim, observe que
$\overrightarrow{GI}=\overrightarrow{GA}+\overrightarrow{AC}+\overrightarrow{CI}=\frac{2}{3}\overrightarrow{MC}+\frac{1}{3}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{CP}=\frac{2}{3}\overrightarrow{MP}+\frac{1}{3}\overrightarrow{AC}=\frac{1}{3}\left( \overrightarrow{BA}+\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BC}\right) =0.$
De maneira análoga, mostramos que $\overrightarrow{GH}=.$ Portanto,
concluímos que $G=H=I,$ e vale as propoções citadas acima.
b) Vamos mostrar que o centro de massa do tetraedro é a interseção das medianas. Sendo assim, seja o tetraedro $ABCD$. A mediana do tetraedro
é definida comos sendo o segmento que une um baricentro de uma das faces do tetraedro, com o seu vértice oposto.
Sejam $A^{\prime },B^{\prime },C^{\prime },D^{\prime }$, sendo respectivamente os baricentros das faces $DBC,$ $ABC,$ $ADC$ e $ADB.$
Observe que $\overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}=0,$ pois $\overrightarrow{D^{\prime }A}+
\overrightarrow{D^{\prime }B}=2\overrightarrow{D^{\prime }P},$ onde $P=\frac{A+B}{2}.$ Como $D^{\prime }$ é o baricentro do triângulo $ABC$, segue que $\overrightarrow{CD^{\prime }=}2\overrightarrow{D^{\prime }P}.$
Assim,
$\overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}=2\overrightarrow{D^{\prime }P}+\overrightarrow{D^{\prime }C}=\overrightarrow{CD^{\prime }}+\overrightarrow{D^{\prime }C}=0.$
Seja $G$ o centro de massa do tetraedro. Uma propriedade dele, é que
$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=0.$
Assim,
$3\overrightarrow{GD^{\prime }}=\overrightarrow{GA}+\overrightarrow{
AD^{\prime }}+\overrightarrow{GB}+\overrightarrow{BD^{\prime }}+
\overrightarrow{GC}+\overrightarrow{CD^{\prime }}=\overrightarrow{GA}+
\overrightarrow{GB}+\overrightarrow{GC}-\left( \overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}\right) =
\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=- \overrightarrow{GD}=\overrightarrow{DG}.$
Portanto, $3\overrightarrow{GD^{\prime }}=\overrightarrow{DG},$ ou seja, o centro de massa $G$ pertence ao segmento $\overrightarrow{DD^{\prime}}.$ De maneira análoga, mostramos que $G$ pertence aos segmentos $\overrightarrow{AA^{\prime }},$ $\overrightarrow{BB^{\prime }}, \overrightarrow{CC^{\prime }}.$ Ou seja, $G$ é o ponto de interseção das medianas.
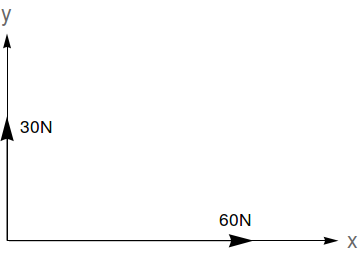
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
Qual é o lugar geométrico de todas as retas que passam pela origem com ângulo diretor em relação ao eixo $z$ $\gamma=30^\circ$?
Um cone sobre o eixo $z$.
Seja $(4,5)$ o ponto médio de um segmento de reta tal que uma extremidade é $(-1,2)$. Ache a outra extremidade.
$(9,8)$.
Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(-1,0,1)$ e sua origem é o ponto médio entre os pontos $P_1=(1,1,3)$ e $P_2=(-1,1,1)$.
$(-1,1,3)$
Ache os dois vetores no plano $xy$ perpendiculares a $4\vec{i}-3\vec{j}$ e de tamanho $10$.
$\pm (6\vec{i}+8\vec{j})$.
Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo às bases e seu comprimento é a média aritmética dos comprimentos das bases.
$\overrightarrow{MN}=\overrightarrow{NB}+\overrightarrow{BA}+\overrightarrow{AM},$ $\overrightarrow{MN}=\overrightarrow{NC}+\overrightarrow{CD}+\overrightarrow{DM}.$ Portanto, $2\overrightarrow{MN}=\overrightarrow{BA}+\overrightarrow{CD}.$
Um vetor no espaço tem dois de seus ângulos diretores dados: $\alpha=45^\circ$ e $\beta=120^\circ$. Ache o outro ângulo diretor e faça um esboço do vetor. Quantas respostas existem? (Sugestão: use as fórmulas de cosseno diretor).
$60^\circ$, $120^\circ$. Existem duas respostas.
Qual é o vetor unitário na direção de $\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}$?
$\dfrac{x\vec{i}+y\vec{j}+z\vec{k}}{\sqrt{x^2+y^2+z^2}}$.
Sejam $\vec{A}$, $\vec{B}$ e $\vec{C}$ vetores no plano, com $\|\vec{A}\|=2$, $\|\vec{B}\|=3$ e $\|\vec{C}\|=4$. O ângulo entre $\vec{A}$ e $\vec{B}$ é de $120^\circ$, entre $\vec{A}$ e $\vec{C}$ é de $135^\circ$ e entre $\vec{B}$ e $\vec{C}$ é de $105^\circ$. Faça um esboço do gráfico desses três vetores. Qual combinação linear de $\vec{A}$ e $\vec{B}$ é igual a $\vec{C}$?
$\vec{C} = -(\sqrt{2}+\sqrt{2/3})\vec{A} + -(4\sqrt{2})/(3\sqrt{3}) \vec{B}$.
Sejam $\vec{A}$, $\vec{B}$ e $\vec{C}$ vetores no plano, com $\|\vec{A}\|=3$, $\|\vec{B}\|=2$ e $\|\vec{C}\|=6$. O ângulo entre $\vec{A}$ e $\vec{B}$ é de $60^\circ$ e $\vec{C}$ está sobre a bissetriz deste ângulo. Faça um esboço do gráfico desses três vetores. Qual combinação linear de $\vec{A}$ e $\vec{B}$ é igual a $\vec{C}$?
$\vec{C} = 2/\sqrt{3} \vec{A} + \sqrt{3} \vec{B}$.
Quais são os cossenos diretores de cada eixo coordenado?
$1,0,0$; $0,1,0$; $0,0,1$.
Mostre que para dois vetores $\vec{A}$ e $\vec{B}$, $\|\vec{A}\| - \|\vec{B}\| \leq \|\vec{A} \pm \vec{B}\| \leq \|\vec{A}\| + \|\vec{B}\|$. Em que condições vale a igualdade?
$\|\vec{A} - \vec{B}\|^2=\|\vec{A}\|^2+\|\vec{B}\|^2- 2\|\vec{A}\|\|\vec{B}\|\cos\theta$.
Dados os pontos $A=(-3,2)$ e $B=(5,4)$:
Faça um esboço de $\vec{AB}$.
Calcule a distância de $A$ até $B$.
Ache o ponto médio entre $A$ e $B$.
Ache o vetor $\vec{BA}$.
Ache o ponto em $\vec{AB}$ cuja distância é 3 vezes maior de $A$ do que de $B$. Isto é, o ponto que divide $\vec{AB}$ na razão $3:1$ (existe outro ponto que está fora de $\vec{AB}$).
Ache o ponto em $\vec{AB}$ cuja coordenada $x$ é igual a $2$.
Ache o ponto em $\vec{AB}$ (extendido) cuja coordenada $y$ é igual a $5$.
Ache os pontos no eixo $x$ e no eixo $y$ que são equidistantes de $A$ e $B$.
Qual é o vetor unitário na direção de $4\vec{i}-12\vec{j}+3\vec{k}$?
$\dfrac{4\vec{i}-12\vec{j}+3\vec{k}}{13}$.
Um vetor no espaço tem dois de seus ângulos diretores dados: $\alpha=30^\circ$ e $\beta=60^\circ$. Ache o outro ângulo diretor e faça um esboço do vetor. Quantas respostas existem? (Sugestão: use as fórmulas de cosseno diretor).
$90^\circ$.
Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(1,1,1)$ e sua extremidade é o ponto $P=(1,1,1)$.
$(0,0,0)$.
Demonstre que se $\alpha$ e $\beta$ são números reais tais que $\alpha(2,3) + \beta(3,2) = \vec{0}$, então $\alpha = 0$ e $\beta = 0$.
Qual a conclusão geométrica que podemos tirar do item acima?
- $\alpha(2,3) + \beta(3,2) = \vec{0}$ resulta no sistema cujas equações são: $2\alpha+3\beta=0$ e $3\alpha+2\beta=0$.
Resolvendo o sistema, obtemos $\alpha=\dfrac{-3}{2}\beta=\dfrac{-2}{3}\beta$ que só pode ser satisfeita se $\beta=0$. E, portanto, $\alpha=0$. - Podemos concluir que esses dois vetores são linearmente independentes, isso significa que eles tem direções distintas.
Quais são os cossenos diretores da reta no plano $xy$ que faz $45^\circ$ com a origem?
$1/\sqrt{2},1/\sqrt{2},0$.
Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores $\alpha_1=45^\circ$, $\beta_1=45^\circ$; e a outra com ângulos diretores $\alpha_2=\beta_2=60^\circ$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).
$45^\circ$.
Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores tais que $\cos\alpha_1=1/2$, $\cos\beta_1=\sqrt{3}/2$; e a outra com ângulos diretores tais que $\cos \alpha_2=\dfrac{\sqrt{3}+1}{2\sqrt{2}}$ e $\cos\beta_2=\dfrac{\sqrt{3}-1}{2\sqrt{2}}$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).
$45^\circ$.
Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores $\alpha_1=\beta_1=60^\circ$; e a outra com ângulos diretores tais que $\cos \alpha_2=\cos \beta_2=1/2\sqrt{2}$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).
$15^\circ$.
Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores tais que $\cos \alpha_1=\cos \beta_1$, $\cos \gamma_1=1/3$; e a outra com ângulos diretores tais que $\cos \alpha_2=\cos \beta_2$, $\cos \gamma_2=1/4$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).
$\cos^{-1} (1/4) - \cos^{-1} (1/3)$.
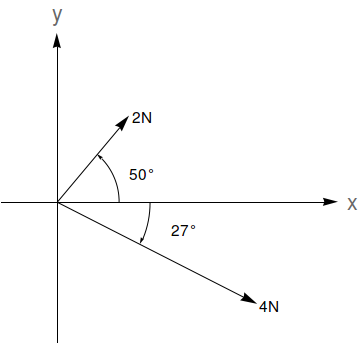
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
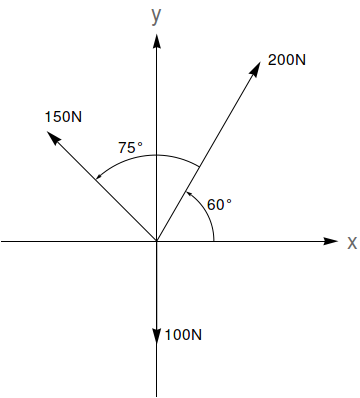
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
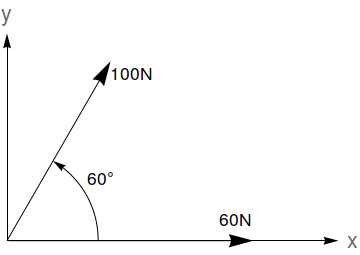
Se $(4,5)$ divide internamente um segmento de reta na razão $3:2$ e uma extremidade é $(-1,2)$, ache a outra extremidade.
$(22/3,7)$, $(23/2,19/2)$ (duas respostas internas).

