Iteradas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Inverta a ordem de integração.
$\displaystyle\int_{-1}^{1}\bigg[\int_{x^{2}}^{\sqrt{2-x^{2}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{y-1}^{2-2y}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{x^{2}}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{-\sqrt{y}}^{\sqrt{y}}f(x,y)\,dx\bigg]dy + \displaystyle\int_{1}^{\sqrt{2}}\bigg[\int_{-\sqrt{2 - y^{2}}}^{\sqrt{2-y^{2}}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{0}\bigg[\int_{0}^{x + 1}f(x,y)\,dy \bigg] dx + \int_{0}^{2}\bigg[\int_{0}^{\frac{2-x}{2}}f(x,y)\,dy \bigg] dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\int_{e^{y-1}}^{e^{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{2x}^{x+1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{\frac{\pi}{4}}\bigg[\int_{0}^{\tan(x)}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{e^{-1}}^{1}\bigg[\int_{0}^{1 + \ln(x)}f(x,y) \ , dy\bigg]dx + \displaystyle\int_{1}^{e}\bigg[\int_{\ln(x)}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{y/2}f(x,y)\,dx\bigg]dy + \int_{1}^{2}\bigg[\int_{y - 1}^{y/2}f(x,y)\,dx\bigg]dy$
$\displaystyle \int_{0}^{1}\bigg[\int_{0}^{\arctan(y)}f(x,y)\,dx \bigg]dy $
Calcule a integral iterada.
$\displaystyle\int_{1}^{4} \int_{1}^{2}\bigg(\dfrac{x}{y}+\dfrac{y}{x}\bigg)\,dy dx$
$\displaystyle\int_{0}^{1} \int_{0}^{3}e^{x+3y}\,dx dy$
$\dfrac{21}{2} \ln(2).$
$\dfrac{(e^{3} - 1)^{2}}{3}.$
Como não há antiderivada elementar da função \(e^{x^2}\), a integral \[ \int_0^2\int_{y/2}^1 e^{x^2}\, dxdy \] não pode ser calculada integrando-se primeiro em relação a \(x\). Calcule essa integral expressando-a como uma integral iterada equivalente com ordem de integração invertida.
A região de integração é dada por \(\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq y\leq 2,\ y/2\leq x\leq 1\}\). Vamos inverter a ordem de integração sobre a região \(R\):\begin{align*} \int_0^2\int_{y/2}^1 e^{x^2}\, dxdy & = \iint\limits_R e^{x^2}\,dA = \int_0^1\int_0^{2x} e^{x^2}\,dydx= \int_0^1\left[e^{x^2}y\right]_{y=0}^{2x}\,dx \\ & = \int_0^1 2xe^{x^2}\,dx = \left.e^{x^2}\right]_0^1 = e-1 \end{align*}
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\int_{\sqrt{x-x^{2}}}^{\sqrt{2x}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{3a}\bigg[\int_{\frac{\sqrt{3}}{3}x}^{\sqrt{4ax-x^{2}}}f(x,y)\,dy\bigg]dx, \; a> 0.$
$\displaystyle\int_{0}^{\pi}\bigg[\int_{0}^{\sin{x}}f(x,y)\,dy\bigg]dx$
$\ \\ \begin{array}{ll} \displaystyle\int_{0}^{\frac{1}{2}}\bigg[\int_{\frac{y^{2}}{2}}^{\frac{1}{2} - \sqrt{\frac{1}{4} - y^{2}}}f(x,y)\,dx\bigg]dy &+ \displaystyle\int_{0}^{\frac{1}{2}}\bigg[\int_{\frac{1}{2}+ \sqrt{\frac{1}{4} - y^{2}}}^{1}f(x,y)\,dx\bigg]dy\\ &+ \displaystyle\int_{\frac{1}{2}}^{\sqrt{2}}\bigg[\int_{\frac{y^{2}}{2}}^{1}f(x,y)\,dx\bigg]dy \end{array} $
$\displaystyle\int_{0}^{\sqrt{3}a} \bigg[\int_{2a + \sqrt{4a^2 - y^{2}}}^{\sqrt{3} y}f(x,y)\,dx\bigg]dy.$
$\displaystyle\int_{0}^{1}\bigg[\int_{\arcsin(y)}^{\pi-\arcsin(y)}f(x,y)\,dx\bigg]dy$
Considere a integral iterada dada por $$\int_{0}^{1} \int_{x}^{\sqrt{x}}\frac{e^{y}}{y}\,dy dx.$$
Desenhe a região de integração no plano $xy.$
Calcule a integral acima.
(...)
$e - 2.$
Cada integral iterada abaixo representa o volume de um sólido. Faça um esboço do sólido. (Não é necessário calcular o volume.)
\(\displaystyle \int_0^5\int_1^2 4\, dxdy\)
\(\displaystyle \int_0^3\int_0^4\sqrt{25-x^2-y^2}\,dydx\)
Determine $\int_{0}^{5}f(x,y)\,dx$ e $\int_{0}^{1}f(x,y)\,dy$, sendo $f(x,y)=12x^{2}y^{3}.$
$\int_{0}^{5} 12x^{2}y^{3} \,dx = 500y^{3}$ e $\int_{0}^{1} 12x^{2}y^{3} \,dy = 3x^{2}.$
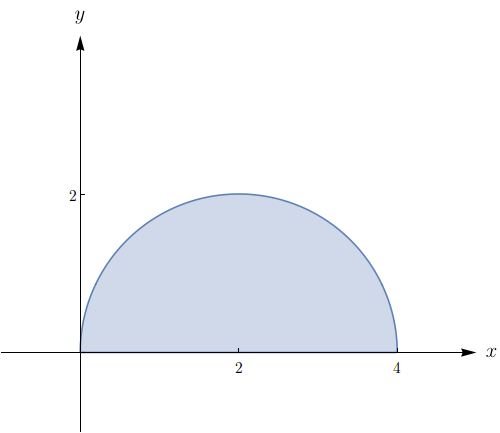
Esboce a região cuja área é dada pela integral e calcule-a, sendo: $\displaystyle\int_{0}^{\pi/2}\int_{0}^{4\cos{\theta}} r \,drd\theta.$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\displaystyle\int_{0}^{x}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{x^{2}}^{x}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{-\sqrt{y}}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\displaystyle\int_{y}^{1}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{y}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{1}\bigg[\int_{x^2}^{1}f(x,y)\,dy\bigg]dx$
Expresse a integral dupla, sobre a região $R$ indicada, como uma integral iterada e ache seu valor.
$\displaystyle\iint\limits_{R}(y+2x)\,dA; \quad R$ região retangular de vértices $(-1,-1)$, $(2,-1)$, $(2,4)$ e $(-1,4).$
$\displaystyle\iint\limits_{R}(x-y)\,dA; \quad R$ região triangular de vértices $(2,9)$, $(2,1)$ e $(-2,1).$
$\displaystyle\iint\limits_{R}xy^{2}\,dA; \quad R$ região triangular de vértices $(0,0)$, $(3,1)$ e $(-2,1).$
$\displaystyle\iint\limits_{R}e^{x/y}\,dA; \quad R$ região limitada pelos gráficos de $y=2x$, $y=-x$ e $y=4.$
$\displaystyle\int_{-1}^{4} \int_{-1}^{2} (y+2x)\,dx;dy = \dfrac{75}{2}.$
$\displaystyle\int_{-2}^{2} \int_{1}^{2x + 5} x - y\,dy;dx = -48.$
$\displaystyle\int_{0}^{1} \int_{-2y}^{3y} xy^{2}\,dx;dy = \dfrac{1}{2}.$
$\displaystyle\int_{0}^{4} \int_{-y}^{y/2} e^{x/y}\,dx;dy = 8(e^{1/2} - e^{-1}).$
Cada integral iterada abaixo representa o volume de um sólido. Faça um esboço do sólido. (Não é necessário calcular o volume.)
\(\displaystyle \int_0^1\int_0^1 (2-x-y)\, dydx\)
\(\displaystyle \int_{-2}^2\int_{-2}^2(x^2+y^2)\,dxdy\)
Calcule a integral iterada.
$\displaystyle\int_{0}^{\pi/2} \int_{0}^{\pi/2}\sin{x}\cos{y} \, dy dx$
$\displaystyle\int_{0}^{2}\!\!\int_{0}^{1}(2x+y)^{8}\,dx dy$
$1.$
$\dfrac{4^{10} - 2^{11}}{180}.$
Suponha que a temperatura, em graus Celsius, num ponto \((x,y)\) de uma chapa metálica plana seja \( T(x,y)=10-8x^2-2y^2 \), onde \(x\) e \(y\) são medidos em metros. Calcule a temperatura média da porção retangular da chapa dada por \(0\leq x\leq 1\) e \(0\leq y\leq 2\).
\(\dfrac{14}{3}\) \({}^\circ\)C
Mude a ordem de integração para mostrar que:
$$ \int_0^a \left[ \int_0^y e^{m(a-x)} f(x) \, dx \right] dy = \int_0^a (a-x) e^{m(a-x)} f(x) \, dx,$$
onde $a$ e $m$ são constantes e $a>0$.
Faça um esboço do sólido no primeiro octante compreendido pelos planos \(x=0\), \(z=0\), \(x=5\), \(z-y=0\) e \(z=-2y+6\).
Calcule o volume do sólido dividindo-o em duas partes.
Inverta a ordem de integração.
$\displaystyle\int_{1}^{e}\bigg[\int_{\ln(x)}^{x}f(x,y)\,dy\bigg]dx.$
$\displaystyle\int_{0}^{1}\bigg[\int_{y}^{y+3}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{1}\bigg[\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{1}^{e^{y}}f(x,y)\,dx\bigg]dy. + \displaystyle\int_{1}^{e}\bigg[\int_{y}^{1}f(x,y)\,dx\bigg]dy.$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{x}f(x,y)\,dy\bigg]dx + \displaystyle\int_{1}^{3}\bigg[\int_{0}^{1}f(x,y)\,dy\bigg]dx + \displaystyle\int_{3}^{4}\bigg[\int_{x-3}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{1}\bigg[\int_{-\sqrt{1-y^{2}}}^{\sqrt{1-y^{2}}}f(x,y)\,dx\bigg]dy$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{\dfrac{\pi}{4}}\bigg[\int_{\sin{x}}^{\cos{x}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{2}\bigg[\int_{\sqrt{\frac{7+5y^{2}}{3}}}^{\frac{y+7}{3}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{3}\bigg[\int_{x^{2}-2x}^{\sqrt{3x}}f(x,y)\,dy\bigg]dx$
$\displaystyle \int_{0}^{\frac{\sqrt{2}}{2}}\bigg[\int_{0}^{\arcsin{y}}f(x,y)\,dx\bigg]dy + \int_{\frac{\sqrt{2}}{2}}^{1}\bigg[\int_{0}^{\arccos{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{2}^{3}\bigg[\int_{3x - 7}^{\sqrt{\frac{3x^2 - 7}{5}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{0}\bigg[\int_{1 - \sqrt{1 + y}}^{1 + \sqrt{1 + y}}f(x,y)\,dx\bigg]dy + \int_{0}^{3}\bigg[\int_{\dfrac{y^{2}}{3}}^{1 + \sqrt{1 + y}}f(x,y)\,dx\bigg]dy$
Calcule a integral iterada.
$\displaystyle\int_{0}^{1}\!\!\int_{0}^{1}(u-v)^{5}\,du dv$
$\displaystyle\int_{0}^{2}\!\!\int_{0}^{\pi}r\sin^{2}{\theta}\,d\theta dr$
$0.$
$\pi.$
Mostre (verifique) que as integrais abaixo podem ser calculadas como:
1. \[ \int_1^5\int_2^{y/2}6x^2y\,dxdy = \int_1^5\left(\dfrac{1}{4}y^4-16y\right)\,dy \]
2. \[ \int_1^5\int_2^{x/2}6x^2y\,dydx = \int_1^5\left(\dfrac{3}{4}x^4-12x^2\right)\,dx \]
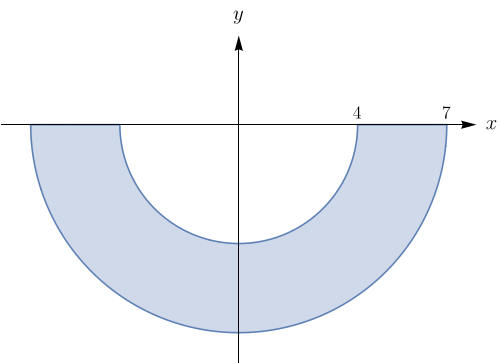
Esboce a região cuja área é dada pela integral e calcule-a, sendo: $\displaystyle\int_{\pi}^{2\pi} \int_{4}^{7} r \, dr d\theta.$
Calcule a integral iterada.
$\displaystyle\int_{1}^{3} \!\! \int_{0}^{1}(1+4xy)\, dx dy$
$\displaystyle\int_{2}^{4}\!\!\int_{-1}^{1}(x^{2}+y^{2})\,dy dx$
$10.$
$\dfrac{116}{3}.$

