Aplicações
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Calcule o volume do conjunto dado.
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1,0\leq z\leq x+2y\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 2, 1\leq y\leq 2, 0\leq z\leq \sqrt{xy}\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1, 0\leq z\leq xye^{x^{2}-y^{2}}\}$
$ \{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1, x^{2}+y^{2}\leq z\leq 2\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 1\leq x\leq 2, 0\leq y\leq 1,\;x+y\leq z\leq x+y+2\}$
$\{(x,y,z)\in \mathbb{R}^{3}|\;0\leq x\leq 1, 0\leq y\leq 1,1\leq z\leq e^{x+y}\}$
$\dfrac{3}{2}.$
$\dfrac{8\sqrt{2}(2\sqrt{2} - 1)}{9}.$
$\dfrac{(e - 1)(1 - e^{-1})}{4}.$
$\dfrac{4}{3}.$
$2.$
$e^{2}-2e.$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq a^{2}$ e $y^{2}+z^{2}\leq a^{2}$, $a >0.$
$x^{2}+y^{2}\leq z\leq 1-x^{2}.$
$\dfrac{16a^{3}}{3}.$
$\dfrac{\pi}{2\sqrt{2}}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo: $\displaystyle D = \{(x,y) \in\mathbb{R}^2: 0 \leq y \leq \sin{(\pi x/L)}, \ 0 \leq x \leq L\}; \quad \rho(x,y) = y$.
Massa: $\dfrac{L}{4};$ centro de massa: $\displaystyle \left(\frac{L}{2},\frac{16}{9\pi} \right).$
Uma carga elétrica é distribuída sobre o retângulo $1 \leq x \leq 3$, $0 \leq y \leq 2$, de modo que a densidade de carga em $(x,y)$ é $\sigma(x,y) = 2xy + y^2$ (medida em coulombs por metro quadrado). Determine a carga total no retângulo.
$\displaystyle \frac{64}{3}$ Coulombs.
Calcule o volume do conjunto dado.
$x^{2}+4y^{2}\leq 4$ e $x+y\leq z\leq x+y+1.$
$x\geq 0$, $x\leq y\leq 1$ e $0\leq z\leq e^{y^{2}}.$
$2\pi.$
$\dfrac{e - 1}{2}.$
Calcule o volume do conjunto dado.
$4x+2y\geq z\geq 3x+y+1$, $x\geq 0$ e $y\geq 0.$
$0\leq z\leq \sin{y^{3}}$ e $\sqrt{x}\leq y\leq \sqrt[3]{\pi}.$
$\dfrac{1}{6}.$
$\dfrac{2}{3}.$
Esboce o sólido cujo volume é dado pela integral iterada
$$\int_{0}^{1} \!\! \int_{0}^{1}(4-x-2y)\, dx dy.$$
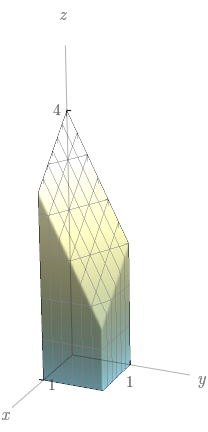
Calcule o volume do conjunto dado.
$0\leq y\leq 1-x^{2}$ e $0\leq z\leq 1-x^{2}.$
$x^{2}+y^{2}+3\leq z\leq 4.$
$\dfrac{16}{15}.$
$\dfrac{\pi}{2}.$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq 1$ e $x+y+2\leq z \leq 4.$
$x\geq 0$, $y \geq 0$, $x+y\leq 1$ e $0\leq z\leq x^{2}+y^{2}.$
$2\pi.$
$\dfrac{1}{6}.$
Verifique que $$f(x,y) = \begin{cases} 4xy, & \quad \text{se } 0 \leq x \leq 1, \ 0 \leq y \leq 1,\\ 0, & \quad \text{caso contrário}, \end{cases}$$ é uma função densidade conjunta.
Se $X$ e $Y$ são variáveis aleatórias cuja função densidade conjunta é a função $f$ do item anterior, determine: (i) $P(X \geq \frac{1}{2})$, (ii) $P(X \geq \frac{1}{2}, Y \leq \frac{1}{2})$.
Determine os valores esperados de $X$ e $Y$.
Note que $$\iint_\limits{\mathbb{R}^2} f(x,y)\,dA = \int_{0}^{1} \int_{0}^{1} 4xy\, dydx = 1. $$
(i) $\dfrac{3}{4}.$ (ii) $\dfrac{3}{16}.$
$\dfrac{3}{16}.$
Utilize a integral dupla para determinar a área da região: limitada pelo eixo $x$ positivo e pela espiral $r=4\theta/3$, $0\leq \theta \leq 2\pi.$ A região se parece com uma concha de caracol.
$\dfrac{64\pi^3}{27}.$
Determine os momentos de inércia da lâmina que ocupa a região $D$ e tem função densidade $\rho$ quando: $D$ é a região triangular delimitada pelas retas $x = 0, \ y = x$ e $2x + y = 6; \quad \rho(x,y) = x^2$.
$\displaystyle I_{x} = \dfrac{1}{16}(e^4 - 1),$ $I_{y} = \dfrac{1}{16}(e^4 - 1)$ e $I_{0} = \dfrac{1}{16}(e^4 + 2e^2 - 3).$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, quando: $D$ é delimitada por $y = e^x$, $y = 0$, $x = 0$ e $x = 1; \quad \rho(x,y) = y$.
Massa: $\dfrac{1}{4}(e^{2} - 1);$ centro de massa: $\displaystyle \left(\frac{e^2 + 1}{2(e^2 - 1)},\frac{4(e^3 - 1)}{9 (e^2 - 1)} \right).$
Calcule o centro de massa da região: $D = \{(x,y) \in \mathbb{R}^2: x^2 + 4y^2 \leq 1, \ y \geq 0\}$ e a densidade é proporcional à distância do ponto ao eixo $x$.
$\displaystyle \left(0, \frac{3\pi}{32} \right).$
Encontre o volume do sólido delimitado pelo parabolóide $z=2+x^{2}+(y-2)^{2}$ e pelos planos $z=1$, $x=1$, $x=-1$, $y=0$ e $y=4.$
Observe que o sólido $E$ está abaixo da superfície $z = 2+x^2+(y-2)^2$ e acima do retângulo $[-1,1]\times [0,4]$ em $z=1$ (ver figura abaixo).
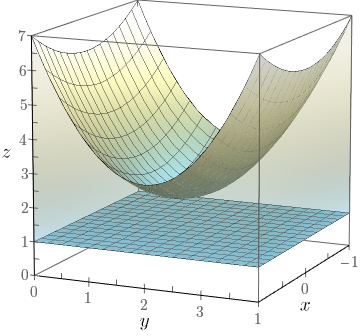
Algebricamente, $$E = \{(x,y,z) \in\mathbb{R}^3: -1 \leq x \leq 1, 0 \leq y \leq 4 \mbox{ e } 1 \leq z \leq 2 + x^2 + (y-2)^2\}.$$ Logo, o volume é dado por $$V = \iint\limits_{R}(2+x^2+(y-2)^2)\,dA - \iint\limits_{ R}\,dA,$$ em que $R = \{(x,y) \in \mathbb{R}^2; -1 \leq x \leq 1 \mbox{ e } 0 \leq y \leq 4 \}$. Assim, \begin{eqnarray*} V & = & \displaystyle\int_{-1}^{1}\int_{0}^{4}(x^2+y^2-4y+5)\,dy dx \\ & = & \displaystyle\int_{-1}^{1} \left.\left(x^2y+\frac{y^3}{3}-2y^2+5y \right|_{y=0}^{y=4} \right) \,dx \\ & = & \displaystyle\int_{-1}^{1} \left(4x^2+\frac{28}{3}\right) \,dx \\ & = & \left.\frac{4x^3}{3}+\frac{28x}{3} \right|_{x=-1}^{x=1} = \frac{64}{3}. \end{eqnarray*} Observe que, pelo Teorema de Fubini, podemos optar por calcular a integral $$\int_{0}^{4}\!\int_{-1}^{1}(x^2+y^2-4y+5)\,dy dx,$$ obtendo o mesmo resultado.
Utilize a integral dupla para determinar a área da região: cortada do primeiro quadrante pela curva $r=2(2-\sin(2\theta))^{1/2}.$
$2(\pi - 1).$
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento $a$, se a densidade em qualquer ponto for proporcional ao quadrado da distância do vértice oposto à hipotenusa.
$\displaystyle \left(\frac{2a}{5}, \frac{2a}{5} \right).$
Uma luminária tem duas lâmpadas de um tipo com tempo de vida médio de 1.000 horas. Supondo que possamos modelar a probabilidade de falha dessas lâmpadas por uma função densidade exponencial com média $\mu = 1.000$, determine a probabilidade de que ambas as lâmpadas venham a falhar dentro de um período de 1.000 horas.
Outra luminária tem somente uma lâmpada do mesmo tipo das do item anterior. Se a lâmpada queima e é trocada por outra to mesmo tipo, determine a probabilidade de que as duas venham a falhar dentro de 1.000 horas.
$(e^{-1} - 1)^2.$
$1 - 2e^{-1}.$
A tendência de uma lâmina de resistir a uma mudança no seu movimento de rotação em torno de um eixo é medida pelo seu momento de inércia em torno daquele eixo. Se a lâmina ocupar uma região \(R\) do plano \(xy\) e se sua densidade \(\delta(x,y)\) for uma função contínua em \(R\), então os momentos de inércia em torno dos eixos \(x\), \(y\) e \(z\) são denotados por \(I_x\), \(I_y\) e \(I_z\), respectivamente, e são definidos por \begin{align*} I_x & = \iint\limits_R y^2\delta(x,y)\,dA, \\ I_y & = \iint\limits_R x^2\delta(x,y)\,dA, \\ I_z & = \iint\limits_R (x^2+y^2)\delta(x,y)\,dA. \\ \end{align*} Considere a lâmina circular que ocupa a região descrita pelas desigualdades \(0\leq x^2+y^2\leq a^2\). Supondo que a lâmina tenha densidade \(\delta\) constante, mostre que \[ I_x= I_y=\dfrac{\delta\pi a^4}{4}, \quad I_z= \dfrac{\delta\pi a^4}{2}.\]
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$ quando: $D$ é a região triangular delimitada pelas retas $x = 0, \ y = x$ e $2x + y = 6; \quad \rho(x,y) = x^2$.
Massa: $4;$ centro de massa: $\displaystyle \left(\frac{6}{5},\frac{12}{5} \right).$
Utilize a integral dupla para determinar a área da região: dentro da cardióide $r=1+\cos{\theta}$ e fora do círculo $r=3\cos{\theta}.$
$\displaystyle \frac{\pi}{4}.$
Utilize o resultado $\displaystyle \int_{-\infty}^{\infty}e^{-x^{2}}\,dx=\sqrt{\pi}$ para calcular as integrais:
$\displaystyle\int_{0}^{\infty} x^{2}e^{-x^{2}}\,dx$
$\displaystyle\int_{0}^{\infty}\sqrt{x}e^{-x}\,dx$
$\displaystyle \frac{\sqrt{\pi}}{4}.$
$\displaystyle \frac{\sqrt{\pi}}{2}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo: $D$ delimitada pelas parábolas $y = x^2$ e $x = y^2; \quad \rho(x,y) = \sqrt{x}$.
Massa: $\dfrac{3}{14};$ centro de massa: $\displaystyle \left(\frac{14}{27},\frac{28}{55} \right).$
Calcule o centro de massa da região: $D$ o triângulo de vértices $(0,0), (0,1)$ e $(1,1)$ e a densidade é proporcional à distância do ponto à origem.
$\displaystyle \left(\frac{3}{4}, \frac{2\sqrt{2} - 1}{2\sqrt{2} + 2\ln(1 + \sqrt{2})} \right).$
Calcule a área limitada pelas curvas $x=y^{2}-1$ e $x=2y^{2}-2.$
$\dfrac{4}{3}.$
A tendência de uma lâmina de resistir a uma mudança no seu movimento de rotação em torno de um eixo é medida pelo seu momento de inércia em torno daquele eixo. Se a lâmina ocupar uma região \(R\) do plano \(xy\) e se sua densidade \(\delta(x,y)\) for uma função contínua em \(R\), então os momentos de inércia em torno dos eixos \(x\), \(y\) e \(z\) são denotados por \(I_x\), \(I_y\) e \(I_z\), respectivamente, e são definidos por \begin{align*} I_x & = \iint\limits_R y^2\delta(x,y)\,dA, \\ I_y & = \iint\limits_R x^2\delta(x,y)\,dA, \\ I_z & = \iint\limits_R (x^2+y^2)\delta(x,y)\,dA. \\ \end{align*} Considere a lâmina retangular que ocupa a região descrita pelas desigualdades \(0\leq x\leq a\) e \( 0\leq y\leq b\). Supondo que a lâmina tenha densidade \(\delta\) constante, mostre que \[ \begin{array}{lll} I_x= \dfrac{\delta ab^3}{3}, & I_y= \dfrac{\delta a^3b}{3}, & I_z= \dfrac{\delta ab(a^2+b^2)}{3}. \end{array} \]
Calcule o centro de massa do quadrado $D$ dado por $0 \leq x \leq 1, \ 0 \leq y \leq 1$ e com densidade $\quad \rho(x,y) = y$.
$\displaystyle \left(\frac{1}{2}, \frac{2}{3} \right).$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq z\leq 2x.$
$x\leq z\leq1-y^{2}$ e $x\geq 0.$
$\dfrac{\pi}{2}.$
$\dfrac{8}{15}.$
Determine o volume do sólido descrito abaixo.
Limitado pelo cilindro $x^{2}+y^{2}=1$ e pelos planos $y=z$, $x=0$ e $z=0$, no primeiro octante.
Cuja base é a região no plano $xy$ que é limitada pela parábola $y=4-x^{2}$ e pela reta $y=3x$, enquanto o topo do sólido é limitado pelo plano $z=x+4.$
No primeiro octante limitado pelos planos coordenados, pelo cilindro $x^{2}+y^{2}=4$ e pelo plano $z+y=3.$
$\dfrac{1}{3}.$
$\dfrac{625}{12}.$
$\dfrac{9\pi - 8}{3}.$
Calcule o centro de massa da região $D$ dada.
$D$ é o conjunto de todos $(x,y)$ tais que $x^3 \leq y \leq x$ e a densidade é constante e igual a 1.
$D$ é o conjunto de todos $(x,y)$ tais que $x \leq y \leq x + 1$, $0 \leq x \leq 1$, e a densidade é o produto das coordenadas do ponto.
$D$ é o conjunto de todos $(x,y)$ tais que $1 \leq x^2 + y^2 \leq 4$, $y \geq 0$, e a densidade é proporcional à distância do ponto à origem.
$\displaystyle \left(0,0\right).$
$\displaystyle \left(\frac{5}{7},\frac{9}{7}\right).$
$\displaystyle \left(0, \frac{45}{14\pi} \right).$
Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for $\rho(x,y) = 1 + 0,1\cdot x$, é mais difícil girar a pá em torno do eixo $x$ ou do eixo $y$?
Se calcularmos os momentos de inércia sobre $x$ e $y$, poderemos determinar em qual direção será mais difíciel de girar a pá do ventilador. Notemos que a região de integração é o quadrado com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem em ambas as integrais. Então, o momento de inércia sobre o eixo $x$ é dada por: $$I_{x}=\iint\limits_{D}y^{2}\rho(x,y)\,dA=\int_{0}^{2}\int_{0}^{2}y^{2}(1+0,1x)dydx$$ $$=\int_{0}^{2}(1+0,1x)\,dx\cdot \int_{0}^{2}y^{2}\,dy=\bigg(x+0,1\frac{x^{2}}{2}\bigg)\bigg|_{0}^{2}\cdot \bigg(\frac{y^{3}}{3}\bigg)\bigg|_{0}^{2}$$ $$=\bigg[(2+0,2)-0\bigg]\cdot \bigg[\frac{8}{3}\bigg]=\frac{17,6}{3}.$$ Da mesma forma, o momente de inércia sobre o eixo $y$ é dado por: $$I_{y}=\iint\limits{D}x^{2}\rho(x,y)\,dA=\int_{0}^{2}\int_{0}^{2}x^{2}(1+0,1x)dydx$$ $$=\int_{0}^{2}(x^{2}+0,1x^{3})\,dx\cdot \int_{0}^{2}\,dy=\bigg(\frac{x^{3}}{3}+0,1\frac{x^{4}}{4}\bigg)\bigg|_{0}^{2}\cdot \bigg(y\bigg)\bigg|_{0}^{2}$$ $$=\bigg[\bigg(\frac{8}{3}+0,4\bigg)-0\bigg]\cdot \bigg[2-0\bigg]=\frac{18,4}{3}.$$ Como $I_{y}>I_{x}$ é mais difícil girarmos a pá do ventilador em torno do eixo $y.$
Determine o volume do sólido limitado pelos planos coordenados e pelo plano $3x+2y+z=6.$
O sólido cujo volume deve ser calculado é $$E = \{(x,y,z) \in \mathbb{R}^3; (x,y) \in R \mbox{ e } 0 \leq z \leq 6 - 3x - 2y\},$$ em que $R$ é a projeção de $E$ no plano $xy$. Assim, o volume é dado por $$V = \displaystyle\int\!\!\!\!\int\limits_{R}(6-3x-2y)\,dA.$$ A região $R$ é tanto do tipo I como do tipo II, então é possível escrevê-la de pelo menos duas formas. Escrevendo como uma região do tipo I, obtemos: $$R = \left\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 2 \mbox{ e } 0 \leq y \leq \frac{6-3x}{2}\right\}.$$ Portanto, \begin{eqnarray*} V & = & \displaystyle\int_{0}^{2}\!\int_{0}^{\frac{6-3x}{2}}(6-3x-2y)\,dy dx \\ & = & \displaystyle\int_{0}^{2} \left.\left(6y-3xy-y^2 \right|_{y=0}^{y=\frac{6-3x}{2}} \right) \,dx \\ & = & \displaystyle\int_{0}^{2} \left(9-9x+\frac{9x^2}{4}\right) \,dx \\ & = & \left.9x-\frac{9x^2}{2}+\frac{9x^3}{12} \right|_{x=0}^{x=2} = 6. \end{eqnarray*} Observe que podemos escrever $R$ como uma região do tipo II, obtendo: $$R = \left\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq \frac{6-2y}{3} \text{ e } 0 \leq y \leq 3\right\}.$$ Então, uma outra expressão para $V$ é $$V = \displaystyle\int_{0}^{3}\!\int_{0}^{\frac{6-2y}{3}}(6-3x-2y)\,dx dy = 6.$$
A função densidade conjunta para um par de variáveis aleatórias $X$ e $Y$ é $$f(x,y) = \begin{cases} Cx(1 + y), & \quad \text{se } 0 \leq x \leq 1, \ 0 \leq y \leq 2,\\ 0, & \quad \text{caso contrário}.
\end{cases}$$
Determine a constante $C$.
Determine $P(X \leq 1, \ Y \leq 1)$.
Determine $P(X + Y \leq 1)$.
$\dfrac{1}{2}.$
$\dfrac{3}{8}.$
$\dfrac{5}{48}$.
Encontre o volume do sólido no primeiro octante limitado pelo cilindro $z=16-x^{2}$ e pelo plano $y=5.$
$\dfrac{640}{3}.$
Determine o valor médio de $f(x,y)=e^{y}\sqrt{x+e^{y}}$ sobre o retângulo $R=[0,4]\times [0,1].$
$\dfrac{(4 + e)^{5/2} - e^{5/2} - 5^{5/2} + 1}{15}.$
A fronteira de uma lâmina consiste nos semicírculos $y = \sqrt{1 - x^2}$ e $y = \sqrt{4 - x^2}$, juntamente com as partes do eixo $x$ que os une. Encontre o centro de massa da lâmina se a densidade em qualquer ponto é proporcional à sua distância da origem.
$\displaystyle \left(0, \frac{45}{14\pi} \right).$
Determine o volume do sólido.
Abaixo do paraboloide $z=x^{2}+y^{2}$ e acima da região delimitada por $y=x^{2}$ e $x=y^{2}.$
Abaixo do paraboloide $z=3x^{2}+y^{2}$ e acima da região delimitada por $y=x$ e $x=y^{2}-y.$
$ $ Abaixo da superfície $z=xy$ e acima do triângulo com vértices $(1,1)$, $(4,1)$ e $(1,2).$
Limitado pelo cilindro $y^{2}+z^{2}=4$ e pelos planos $x=2y$, $x=0$ e $z=0$, no primeiro octante.
$\dfrac{6}{35}.$
$\dfrac{144}{35}.$
$\dfrac{31}{8}.$
$\dfrac{16}{3}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo:$D$ a região triangular com vértices $(0,0), (2,1), (0,3)$ e $\rho(x,y) = x + y$.
Massa: $6;$ centro de massa: $\displaystyle \left(\frac{3}{4},\frac{3}{2} \right).$
Utilize a integral dupla para determinar a área da região: um laço da rosácea $r=\cos(3\theta).$
$\displaystyle \frac{\pi}{12}.$
Calcule o volume do conjunto dado.
$x+y+z\leq 1$, $x\geq 0$, $y\geq 0$ e $z\geq 0.$
$x\leq y\leq 1$, $x\geq 0$, $z\geq 0$ e $z^{2}+x^{4}+x^{2}y^{2}\leq 2x^{2}.$
$\dfrac{1}{6}.$
$\dfrac{\pi(1 - \sqrt{2})}{8} + \dfrac{1}{3}.$
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste a oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade norte. Encontre o volume de água da piscina.
$1800 \pi$ m$^3.$
Uma lâmina ocupa parte do disco $x^2 + y^2 \leq 1$ no primeiro quadrante. Determine o centro de massa se a densidade em qualquer ponto for proporcional à distância do ponto ao eixo $x$.
$\displaystyle \left(\frac{3}{8}, \frac{3\pi}{16} \right).$
Determine a massa e o centro de massa da lâmina que ocupa a região $\displaystyle D = \{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 2, \ -1 \leq y \leq 1\}$ e tem função densidade $\rho(x,y) = xy^2.$
Massa: $\dfrac{4}{3};$ centro de massa: $\displaystyle \left(\frac{4}{3},0 \right).$
Utilize a integral dupla para determinar a área da região: no interior do círculo $x^{2}+(y-1)^{2}=1$ e fora do círculo $x^{2}+y^{2}=1.$
$\displaystyle \frac{\pi}{3} + \frac{\sqrt{3}}{2}.$

