Derivada das funções exponenciais e logarítmicas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Seja $g(x)=log_a{x}$, em que $a>0$ e $a \neq 1$ é um real dado. Mostre que $g'(x)=\dfrac{1}{x \ln{a}}$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =2^{x}$.
$f'(x)=ln(2)2^x$.
Determine a equação da reta tangente ao gráfico de $f(x)=\ln{x}$ no ponto de abscissa $1$. Esboce os gráficos de $f$ e da reta tangente.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{\ln x}{x}$.
$f'(x)=1-ln(x)$.
Considere as funções trigonométricas hiperbólicas:
\begin{equation*} \sinh x=\dfrac{e^{x}-e^{-x}}{2};\;\cosh x=\dfrac{e^{x}+e^{-x}}{2}\text{.} \end{equation*}
Mostre que $\cosh ^{2}x-\sinh ^{2}x=1$.
Mostre que $\left( \sinh ^{\prime }x\right) ^{2}-\left( \cosh^{\prime }x\right) ^{2}=1$.
Usa-se a técnica do carbono-14 para determinar a idade de espécimes arqueológicos ou geológicos. Este método baseia-se no fato de que o carbono-14, isótopo instável ($^{14}C$) está presente no $CO_2$ na atmosfera. As plantas assimilam carbono da atmosfera; quando morrem o $^{14}C$ acumulado começa a decair, com uma meia vida de aproximadamente 5700 anos. Medindo-se a quantidade de $^{14}C$ que resta em um espécime, é possível determinar quando o organismo morreu. Suponha que um osso fóssil acuse 20\% da quantidade de $^{14}C$ presente em um osso dos dias atuais. Dê uma aproximação da idade do osso fóssil.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\pi ^{x}$.
$f'(x)=ln(\pi)\pi^x$.
O modelo Jenss é considerado geralmente como a fórmula mais precisa para predizer a altura de uma criança em idade pré-escolar. Se $h(x)$ denota a altura (em cm) na idade $x$ (em anos) para $\frac{1}{4} \leq x \leq 6$, então $h(x)$ pode ser aproximada por $h(x)=79,041+6,39x-e^{3,261-0,993x}$.
- Preveja a altura e a taxa de crescimento quando uma criança atinge a idade de $1$ ano.
- Quando é maior e quando é menor a taxa de crescimento?
Para uma população de elefantas africanas, o peso $W(t)$ (em quilogramas) e a idade $t$ (em anos) pode ser aproximado por uma função de crescimento de Fertanlanffy $W$ tal que $W(t)=2600(1-0,51e^{-0,075t})^3$.
- Dê uma aproximação do peso e da taxa de crescimento de um elefante recém-nascido.
- Supondo que uma elefanta adulta pese $1800$ $kg$, estime sua idade e sua taxa de crescimento presente.
- Calcule e interprete $\lim\limits_{t \to \infty}W(t)$.
- Mostre que a taxa de crescimento é máxima entre as idades de $5$ e $6$ anos.
Se um raio de luz de intensidade $k$ é projetado verticalmente para baixo na água, então a sua intensidade $I(x)$ à profundidade de $x$ metros é $I(x)=ke^{-1,4x}$.
- A que taxa de intensidade o raio de luz está variando em relação à profundidade a $1$ metro?
- A que profundidade a intensidade é a metade de seu valor na superfície?
As distribuições gamma, importantes em teoria das probabilidades, são determinadas por $f(x)=cx^ne^{-ax}$ para $x>0$, um inteiro positivo $n$, uma constante positiva $a$ e $c=\dfrac{a^{n+1}}{n!}$.
- Mostre que $f$ tem exatamente um máximo local.
- Supondo $n=4$, determine onde $f(x)$ cresce mais rapidamente.
Seja $g(x)=a^x$, em que $a>0$ e $a \neq 1$ é um real dado. Mostre que $g'(x)=a^x \ln{a}$.
Se $p$ denota o preço de venda de um artigo e $x$ é a procura correspondente (em número de artigos vendidos por di, então a relação entre $p$ e $x$ pode ser dada por $p(x)=p_0e^{-ax}$ para constantes positivas $p_0$ e $a$. Suponha $p(x)=300e^{-0,02x}$. Determine o preço de venda que maximize a receita diária.
A taxa de crescimento $R$ de certo tipo de tumor pode ser relacionada com seu tamanho $x$, de modo aproximado, pela equação $R=r\cdot x\cdot ln(K/x)$, em que $r$ e $K$ são constantes positivas. Mostre que o tumor cresce mais rapidamente quando $x=e^{-1}K$.
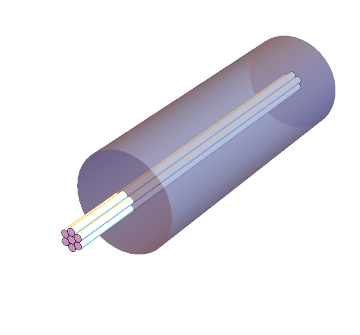
Os impulsos nervosos no corpo humano caminham ao longo de fibras nervosas que consistem em um axônio, que transporta o impulso, envolvido por uma camada de mielina. A fibra nervosa é semelhante a um cabo cilíndrico isolado, para o qual a velocidade $v$ de um impulso é dada por $v=-k(r/R)^2 \ln(r/R)$, onde $r$ é o raio do cabo e $R$ é o raio de isolamento. Ache o valor de $r/R$ que maximize $v$. Na maioria das fibras nervosas, $r/R$ vale aproximadamente $0,6$.
Um modelo de densidade urbana é uma fórmula que relaciona a densidade populacional (em número de habitantes por $km^2$) com a distância $r$ (em $km$) do centro da cidade. É considerada apropriada para certas cidades a fórmula $D=ae^{-br+cr^2}$, com $a,b$ e $c$ constantes positivas. Determine a forma do gráfico de $D$ para $r \geq 0$.
Se uma droga é injetada em uma corrente sanguínea, sua concentração $C$, $t$ minutos depois, é dada por $C(t)=\frac{k}{a-b}(e^{-bt}-e^{-at})$, para constantes positivas $a$, $b$ e $k$.
- Em que instante ocorre a concentração máxima?
- Que se pode dizer sobre a concentração após um longo período de tempo?
A corrente $I(t)$ em um circuito elétrico composto de um resistor e um indutor, no instante $t$, é dada por $I(t)=I_0e^{-Rt/L}$, onde $R$ é a resistência, $L$ a indutância e $I_0$ é a corrente no instante $t=0$. Mostre que a taxa de variação da corrente no instante $t$ é proporcional a $I(t)$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\log _{a}x,\;a>0$ e $a\neq 1$.
$f'(x)=\dfrac{1}{xln(a)}
Determine a equação da reta tangente ao gráfico de $f(x)=e^x$ no ponto de abscissa $0$.
Um invertimento de \$500,00 da juro de 7% ao ano, capitalizado continuamente, e apót $t$ anos o investimento valerá $500e^{0,07t}$.
- Aproximadamente, quando o investimento valerá \$1000,00?
- Quando o valor do investimento estará crescendo à razão de \$50,00 por ano?
Uma substância radioativa decai de acordo com a fórmula $q(t)=q_0e^{-ct}$, onde $q_0$ é a quantidade inicial da substância, $c$ é uma constante positiva, e $q(t)$ é a quantidade remanescente após o tempo $t$. Mostre que a taxa na qual a substância decai é proporcional a $q(t)$.

